
分析 (I)根据f(x)=$\overrightarrow{m}•\overrightarrow{n}$,根据向量乘积的运算,可得f(x)的解析式,化简后.将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;
(II)根据f(A)=1,求解A的大小.利用余弦定理求解bc的值,可得△ABC的面积.
解答 解:(Ⅰ)知$\overrightarrow m=({\sqrt{3}sinx,cosx}),\overrightarrow n=({cosx,cosx}),x∈R,设f(x)=\overrightarrow m•\overrightarrow n$.
∴$f(x)=\sqrt{3}sinx•cosx+{cos^2}x$=$\frac{{\sqrt{3}}}{2}sin2x+\frac{1+cos2x}{2}$=$sin(2x+\frac{π}{6})+\frac{1}{2}$.
∴f(x)的解析式:f(x)=sin(2x+$\frac{π}{6}$)$+\frac{1}{2}$.
令$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ⇒-\frac{π}{3}+kπ≤x≤\frac{π}{6}+kπ,(k∈Z)$
∴f(x)的单调递增区间为$[-\frac{π}{3}+kπ,\frac{π}{6}+kπ]\;(k∈Z)$
(Ⅱ)由$f(A)=sin(2A+\frac{π}{6})+\frac{1}{2}=1⇒sin(2A+\frac{π}{6})=\frac{1}{2}$,
又∵A∈(0,π),
∴$2A+\frac{π}{6}∈(\frac{π}{6},\frac{13π}{6})$
∴$2A+\frac{π}{6}=\frac{5π}{6}⇒A=\frac{π}{3}$
由余弦定理,可得a2=b2+c2-2bc•cosA=(b+c)2-2bc•(1+cosA)
∴bc=1,
∴${S_{△ABC}}=\frac{1}{2}bc•sinA=\frac{{\sqrt{3}}}{4}$.
点评 本题考查了向量乘积的运算,正余弦函数的运用,三角函数的图象和性质,考查了计算能力,属于中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源:2015-2016学年陕西省高一下学期期末考数学试卷(解析版) 题型:选择题
甲、乙两人在相同的条件下各射靶10次,他们的环数的方差分别为: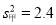 ,
,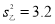 ,则射击稳定程度是
,则射击稳定程度是
A.甲高 B.乙高 C.两人一样高 D.不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -$\frac{1}{2}$ | C. | -2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com