
【题目】【2015高考四川,文21】已知函数f(x)=-2lnx+x2-2ax+a2,其中a>0.
(Ⅰ)设g(x)为f(x)的导函数,讨论g(x)的单调性;
(Ⅱ)证明:存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
【答案】见解析
【解析】(Ⅰ)由已知,函数f(x)的定义域为(0,+∞)
g(x)=f '(x)=2(x-1-lnx-a)
所以g'(x)=2-![]()
当x∈(0,1)时,g'(x)<0,g(x)单调递减
当x∈(1,+∞)时,g'(x)>0,g(x)单调递增
(Ⅱ)由f '(x)=2(x-1-lnx-a)=0,解得a=x-1-lnx
令Φ(x)=-2xlnx+x2-2x(x-1-lnx)+(x-1-lnx)2=(1+lnx)2-2xlnx
则Φ(1)=1>0,Φ(e)=2(2-e)<0
于是存在x0∈(1,e),使得Φ(x0)=0
令a0=x0-1-lnx0=u(x0),其中u(x)=x-1-lnx(x≥1)
由u'(x)=1-![]() ≥0知,函数u(x)在区间(1,+∞)上单调递增
≥0知,函数u(x)在区间(1,+∞)上单调递增
故0=u(1)<a0=u(x0)<u(e)=e-2<1
即a0∈(0,1)
当a=a0时,有f '(x0)=0,f(x0)=Φ(x0)=0
再由(Ⅰ)知,f '(x)在区间(1,+∞)上单调递增
当x∈(1,x0)时,f '(x)<0,从而f(x)>f(x0)=0
当x∈(x0,+∞)时,f '(x)>0,从而f(x)>f(x0)=0
又当x∈(0,1]时,f(x)=(x-a0)2-2xlnx>0
故x∈(0,+∞)时,f(x)≥0
综上所述,存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:高中数学 来源: 题型:
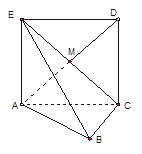
【题目】如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,![]() ,且AC=BC.
,且AC=BC.
(1)求证:![]() 平面EBC;
平面EBC;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为![]() ,答对文科题的概率均为
,答对文科题的概率均为![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届广东省珠海市高三上学期期末考试文数】已知函数![]() 的最小值为0,其中
的最小值为0,其中![]() ,设
,设![]() .
.
(1)求![]() 的值;
的值;
(2)对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)讨论方程![]() 在
在![]() 上根的个数.
上根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2014福建,文22】已知函数![]() (
(![]() 为常数)的图像与
为常数)的图像与![]() 轴交于点
轴交于点![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
(1)求![]() 的值及函数
的值及函数![]() 的极值;
的极值;
(2)证明:当![]() 时,
时,![]()
(3)证明:对任意给定的正数![]() ,总存在
,总存在![]() ,使得当
,使得当![]() 时,恒有
时,恒有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2014高考陕西版文第21题】设函数![]() .
.
(1)当![]() (
(![]() 为自然对数的底数)时,求
为自然对数的底数)时,求![]() 的最小值;
的最小值;
(2)讨论函数![]() 零点的个数;
零点的个数;
(3)若对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() (其中
(其中![]() )满足下列3个条件:
)满足下列3个条件:
①函数![]() 的图象过坐标原点;
的图象过坐标原点;
②函数![]() 的对称轴方程为
的对称轴方程为![]() ;
;
③方程![]() 有两个相等的实数根,
有两个相等的实数根,
令![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求使不等式![]() 恒成立的实数
恒成立的实数![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 在平面直角坐标系
在平面直角坐标系![]() 下的参数方程为
下的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的普通方程及极坐标方程;
的普通方程及极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
: ![]() 与曲线
与曲线![]() 交于点
交于点![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com