
如图是一个空间几何体的三视图,则该几何体的外接球的表面积为( )
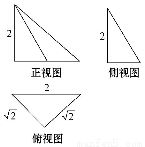
(A)8π (B)6π (C)4π (D)2π
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC,点E是棱PB上的动点.
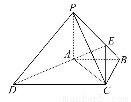
(1)若PD∥平面EAC,试确定点E在棱PB上的位置.
(2)在(1)的条件下,求二面角A-CE-P的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷(解析版) 题型:选择题
一个水平放置的平面图形的斜二测直观图是直角梯形 (如图所示),∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( )
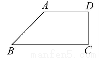
(A) +
+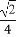 (B)2+
(B)2+
(C) +
+ (D)
(D) +
+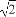
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷(解析版) 题型:填空题
正四棱锥S-ABCD中,O为顶点在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC所成的角等于 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷(解析版) 题型:选择题
在正方体ABCD-A1B1C1D1中,二面角A1-BD-C1的余弦值为( )
(A)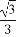 (B)
(B)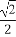 (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:解答题
如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A-BB1D1D的体积为 cm3.
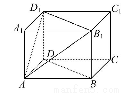
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:选择题
某几何体的三视图如图所示,且正视图、侧视图都是矩形,则该几何体的体积是( )
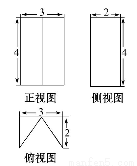
(A)16 (B)12 (C)8 (D)6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:选择题
已知向量a=(1,-1,1),b=(-1,2,1),且ka-b与a-3b互相垂直,则k的值是( )
(A)1 (B) (C)
(C) (D)-
(D)-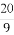
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十第二章第七节练习卷(解析版) 题型:选择题
函数f(x)=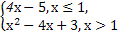 的图象和g(x)=log2x的图象的交点个数是( )
的图象和g(x)=log2x的图象的交点个数是( )
(A)4 (B)3 (C)2 (D)1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com