
(本题12分)一个质地均匀的正四面体的四个面上分别标示着数字1、2、3、4,一个质地均匀的骰子(正方体)的六个面上分别标示数字1、2、3、4、5、6,先后抛掷一次正四面体和骰子。
⑴列举出全部基本事件;
⑵求被压在底部的两个数字之和小于5的概率;
⑶求正四面体上被压住的数字不小于骰子上被压住的数字的概率。
⑴ 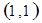
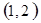
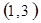
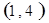
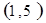

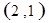
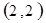
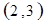
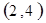
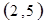
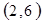
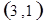
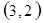
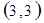
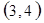
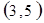


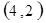
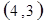
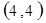
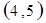

每个基本事件出现的可能性相同.
⑵ 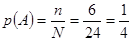 .
.
⑶ 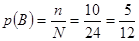 .
.
解析试题分析:⑴ 用数对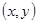 标示正四面体上和骰子上被压住的两个数字,列举所有基本事件如下:
标示正四面体上和骰子上被压住的两个数字,列举所有基本事件如下: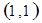
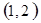
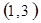
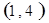
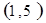

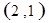
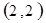
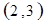
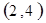
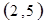
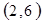
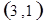
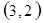
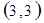
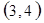
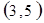


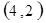
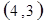
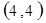
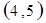

每个基本事件出现的可能性相同. …………………………4分
⑵ 由⑴知基本事件总数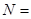 24.
24.
设“被压在底部的两个数字之和小于5”为事件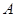 ,则
,则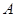 包括
包括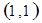 、
、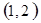 、
、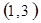 、
、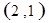 、
、 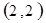 、
、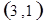 等6个基本事件,事件
等6个基本事件,事件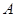 发生的概率
发生的概率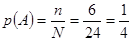 . ………8分
. ………8分
⑶ 设“正四面体上被压住的数字不小于骰子上被压住的数字”为事件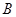 ,则
,则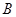 包括
包括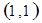 、
、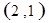 、
、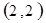 、
、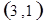 、
、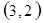 、
、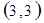 、
、 、
、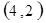 、
、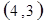 、
、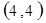 等10个基本事件,事件
等10个基本事件,事件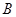 发生的概率
发生的概率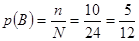 . ……………………………………12分
. ……………………………………12分
考点:本题主要考查古典概型概率的计算。
点评:基础题,古典概型概率的计算,公式明确,关键是计算基本事件数要准确,可借助于“树图法”“坐标法”。


科目:高中数学 来源: 题型:解答题
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨
标准煤)的几组对照数据:
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程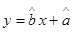 ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产
l00吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5="66.5"
用最小二乘法求线性回归方程系数公式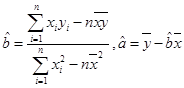 ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是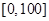 ,样本数据分组为
,样本数据分组为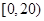 ,
,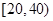 ,
,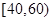 ,
,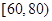 ,
,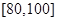 .
.
(Ⅰ)求直方图中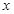 的值;
的值;
(Ⅱ)如果上学所需时间不少于1小时的学生可申请在学校住宿,请估计学校600名新生中有多少名学生可以申请住宿;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据。
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
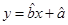 ;
;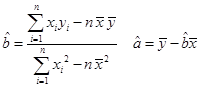 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分) 某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少
某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少 的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .若备选的5个居民小区中有三个非低碳小区,两个低碳小区.
的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .若备选的5个居民小区中有三个非低碳小区,两个低碳小区.
(1)求所选的两个小区恰有一个为“非低碳小区”的概率;
(2)假定选择的“非低碳小区”为小区 ,调查显示其“低碳族”的比例为1:2,数据如图1所示,经过大力宣传,三个月后又进行一次调查,数据如图2所示,问这时小区
,调查显示其“低碳族”的比例为1:2,数据如图1所示,经过大力宣传,三个月后又进行一次调查,数据如图2所示,问这时小区 是否达到“低碳小区”的标准?
是否达到“低碳小区”的标准?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
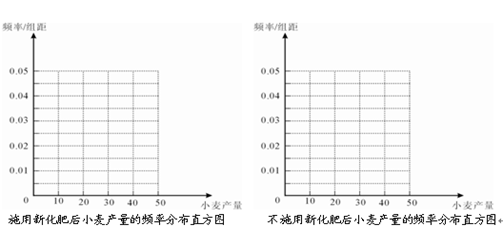
(本题12分)为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200个 的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
表1:施用新化肥小麦产量频数分布表
| 小麦产量 |  | 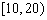 | 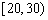 | 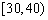 | 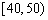 |
| 频数 | 10 | 35 | 40 | 10 | 5 |
| 小麦产量 | 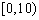 | 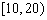 | 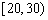 | 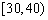 |
| 频数 | 15 | 50 | 30 | 5 |
| | 小麦产量小于20kg | 小麦产量不小于20kg | 合计 |
| 施用新化肥 | 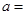 | 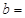 | |
| 不施用新化肥 | 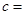 |  | |
| 合计 | | | 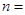 |
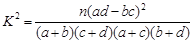
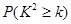 | 0.050 | 0.010 | 0.005 | 0.001 |
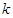 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
| | 文艺节目 | 新闻节目 | 总计 |
| 20至40岁 | 40 | 10 | 50 |
| 大于40岁 | 20 | 30 | 50 |
| 总计 | 60 | 40 | 100 |
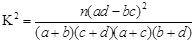
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)为了调查甲、乙两个交通站的车流量,随机选取了14天,统计每天上午8∶00~12∶00间各自的车流量(单位:百辆),得如图所示的统计图,试求: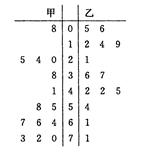
(1)甲、乙两个交通站的车流量的极差分别是多少?
(2)甲交通站的车流量在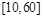 间的频率是多少?
间的频率是多少?
(3)根据该茎叶图结合所学统计知识分析甲、乙两个交通站哪个站更繁忙?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5 月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图),已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请回答下列问题:
(1)本次活动共有多少件作品参加评比?
(2)经过评比,第四组和第六组分别有10件和2件 作品获奖,问这两组哪组获奖率更高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com