
【题目】在三棱柱![]() 中,底面
中,底面![]() 是等腰三角形,且
是等腰三角形,且![]() ,侧面
,侧面![]() 是菱形,
是菱形,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
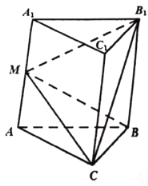
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知圆![]() ,点
,点![]() ,
,![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线与半径
的垂直平分线与半径![]() 相交于点
相交于点![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() 。
。
(1)求曲线![]() 的方程;
的方程;
(2)若![]() ,设过点
,设过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 分别交于点
分别交于点![]() ,其中
,其中![]() ,求证:直线
,求证:直线![]() 必过
必过![]() 轴上的一定点。(其坐标与
轴上的一定点。(其坐标与![]() 无关)
无关)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全国第五个“扶贫日”到来之前,某省开展“精准扶贫,携手同行”的主题活动,某贫困县调查基层干部走访贫困户数量.![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从
镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从![]() 三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,
三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
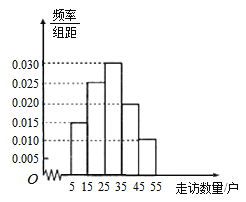
(1)求这40人中有多少人来自![]() 镇,并估计
镇,并估计![]() 三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
(2)如果把走访贫困户达到或超过25户视为工作出色,以频率估计概率,从![]() 三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为
三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市自2014年至2019年每年年初统计得到的人口数量如表所示.
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人数(单位:万) | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)设第![]() 年的人口数量为
年的人口数量为![]() (2014年为第1年),根据表中的数据,描述该城市人口数量和2014年至2018年每年该城市人口的增长数量的变化趋势;
(2014年为第1年),根据表中的数据,描述该城市人口数量和2014年至2018年每年该城市人口的增长数量的变化趋势;
(2)研究统计人员用函数![]() 拟合该城市的人口数量,其中
拟合该城市的人口数量,其中![]() 的单位是年.假设2014年初对应
的单位是年.假设2014年初对应![]() ,
,![]() 的单位是万.设
的单位是万.设![]() 的反函数为
的反函数为![]() ,求
,求![]() 的值(精确到0.1),并解释其实际意义.
的值(精确到0.1),并解释其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国国际智能产业博览会(智博会)每年在重庆市举办一届,每年参加服务的志愿者分“嘉宾”、“法医”等若干小组![]() 年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出50人作为2019年中国国际智博会服务的志愿者.
年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出50人作为2019年中国国际智博会服务的志愿者.
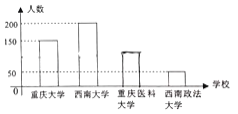
(1)若“嘉宾”小组需要2名志愿者,求这2人分别来自不同大学的概率(结果用分数表示)
(2)若“法医”小组的3名志愿者只能从重庆医科大学或西南政法大学抽出,用![]() 表示抽出志愿者来自重庆医科大学的人数,求
表示抽出志愿者来自重庆医科大学的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到直线
到直线![]() 的距离比到定点
的距离比到定点![]() 的距离大1.
的距离大1.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)若![]() 为直线
为直线![]() 上一动点,过点
上一动点,过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() ,
,![]() ,切点为
,切点为![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
①求证:![]() 轴;
轴;
②直线![]() 是否恒过一定点?若是,求出这个定点的坐标;若不是,请说明理由.
是否恒过一定点?若是,求出这个定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上任意一点,
上任意一点,![]() ,且点
,且点![]() 为线段
为线段![]() 的中点.
的中点.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若![]() 为点
为点![]() 关于原点
关于原点![]() 的对称点,过
的对称点,过![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 、
、![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于点
于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com