
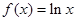 ,
,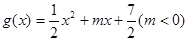 ,直线
,直线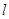 与函数
与函数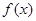 、
、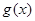 的图象都相切,且与函数
的图象都相切,且与函数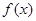 的图象的切点的横坐标为
的图象的切点的横坐标为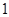 .
.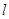 的方程及
的方程及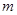 的值;
的值;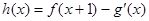 (其中
(其中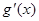 是
是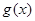 的导函数),求函数
的导函数),求函数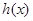 的最大值;
的最大值;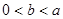 时,求证:
时,求证: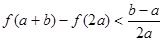 .
.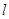 的方程为
的方程为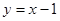 .
.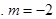 .
.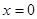 时,
时,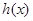 取最大值,其最大值为2.
取最大值,其最大值为2.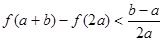
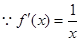 ,
,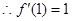 .∴直线
.∴直线 的斜率为
的斜率为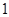 ,且与函数
,且与函数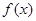 的图象的切点坐标为
的图象的切点坐标为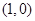 . ∴直线
. ∴直线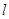 的方程为
的方程为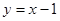 . 又∵直线
. 又∵直线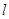 与函数
与函数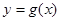 的图象相切,
的图象相切,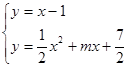 有一解. 由上述方程消去
有一解. 由上述方程消去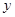 ,并整理得
,并整理得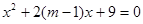 ①
①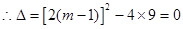
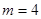 或
或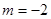
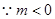
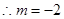 .
.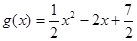 ,
,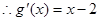
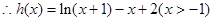 .
. 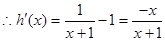 .
. 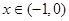 时,
时,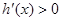 ,当
,当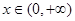 时,
时,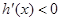 .
.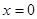 时,
时,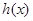 取最大值,其最大值为2.
取最大值,其最大值为2.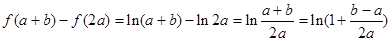 .
. 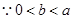 ,
, 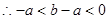 ,
, 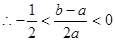 .
.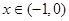 时,
时,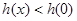 ∴当
∴当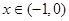 时,
时,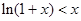 ,
,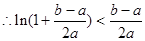 . ∴
. ∴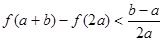


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com