
请观察以下三个式子:
① ;
;
② ;
;
③ ,
,
归纳出一般的结论,并用数学归纳法证明之.
科目:高中数学 来源: 题型:解答题
若函数 满足:集合
满足:集合 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数 是等比源函数.
是等比源函数.
(1)判断下列函数:① ;②
;② 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(2)证明:对任意的正奇数 ,函数
,函数 不是等比源函数;
不是等比源函数;
(3)证明:任意的 ,函数
,函数 都是等比源函数.
都是等比源函数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
先阅读下列不等式的证法,再解决后面的问题:
已知a1,a2∈R,a1+a2=1,求证: +
+ ≥
≥ .
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2,f(x)对一切实数x∈R,恒有f(x)≥0,则Δ=4-8( +
+ )≤0,∴
)≤0,∴ +
+ ≥
≥ .
.
(1)已知a1,a2,…,an∈R,a1+a2+…+an=1,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设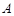 是由
是由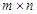 个实数组成的
个实数组成的 行
行 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(Ⅰ) 数表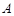 如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
表1
| 1 | 2 | 3 |  |
 | 1 | 0 | 1 |
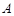 如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数
如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数 的所有可能值;
的所有可能值;
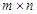 个实数组成的
个实数组成的 行
行 列的任意一个数表
列的任意一个数表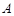 ,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由.
,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com