
【题目】已知![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为轴将
为轴将![]() 旋转
旋转![]() 到
到![]() ,形成三棱锥
,形成三棱锥![]() .
.
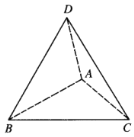
(Ⅰ)求证:![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() 及
及![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .证明
.证明![]() 平面
平面![]() ,即得
,即得![]() ,再由平面几何知识得
,再由平面几何知识得![]() ,由
,由![]() 可得线面垂直,从而得证线线垂直;
可得线面垂直,从而得证线线垂直;
(Ⅱ)作出直线与平面所成的角,通过解三角形求解.
(Ⅰ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() 及
及![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .则
.则![]() ,
,
∵![]() ,∴
,∴![]() ,由旋转知
,由旋转知![]() ,
,
∴二面角![]() 的平面角即为
的平面角即为![]() ,
,
且![]() ,∴
,∴![]() 平面
平面![]() ,
,
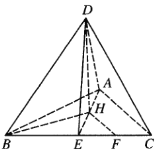
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
∵![]() ,
,![]() ,
,
∴![]() 为正三角形,∴
为正三角形,∴![]() .
.
∵平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
易求得![]() ,
,![]() ,
,![]() ,
,
由![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,从而
,从而![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ∴
∴![]() .
.
(Ⅱ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() 边上的高,垂足为
边上的高,垂足为![]() .
.
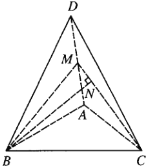
∵![]() ,又
,又![]() ,且
,且![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() ,且
,且![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴直线![]() 与平面
与平面![]() 所成的角即为
所成的角即为![]() ,
,
由(Ⅰ)可知![]() 为正三角形,可知
为正三角形,可知![]() ,
,
则易求得![]() ,
,![]() ,
,
∴![]() ,则
,则![]() ,
,
即直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】2020年是全面建成小康社会目标实现之年,也是全面打赢脱贫攻坚战收官之年.某乡镇在2014年通过精准识别确定建档立卡的贫困户共有500户,结合当地实际情况采取多项精准扶贫措施,每年新脱贫户数如下表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
脱贫户数 | 55 | 68 | 80 | 92 | 100 |
(1)根据2015-2019年的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测到2020年底该乡镇500户贫困户是否能全部脱贫;
,并预测到2020年底该乡镇500户贫困户是否能全部脱贫;
(2)2019年的新脱贫户中有20户五保户,20户低保户,60户扶贫户.该乡镇某干部打算按照分层抽样的方法对2019年新脱贫户中的5户进行回访,了解生产生活、帮扶工作开展情况.为防止这些脱贫户再度返贫,随机抽取这5户中的2户进行每月跟踪帮扶,求抽取的2户不都是扶贫户的概率.
参考公式: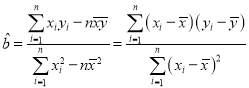 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ex﹣ax2﹣ax,h(x)=ex﹣2x﹣lnx.其中e为自然对数的底数.
(1)若f(x)=h(x)﹣g(x).
①讨论f(x)的单调性;
②若函数f(x)有两个不同的零点,求实数a的取值范围.
(2)已知a>0,函数g(x)恰有两个不同的极值点x1,x2,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线上一点(
为抛物线上一点(![]() 在
在![]() 轴上方),
轴上方),![]() ,
,![]() 点到
点到![]() 轴的距离为4.
轴的距离为4.
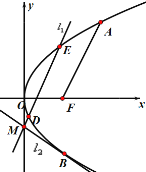
(1)求抛物线方程及点![]() 的坐标;
的坐标;
(2)是否存在![]() 轴上的一个点
轴上的一个点![]() ,过点
,过点![]() 有两条直线
有两条直线![]() ,满足
,满足![]() ,
,![]() 交抛物线
交抛物线![]() 于
于![]() 两点.
两点.![]() 与抛物线相切于点
与抛物线相切于点![]() (
(![]() 不为坐标原点),有
不为坐标原点),有![]() 成立,若存在,求出点
成立,若存在,求出点![]() 的坐标.若不存在,请说明理由.
的坐标.若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个微信群某次进行的抢红包活动中,群主所发红包的总金额为10元,被随机分配为2.49元、1.32元、2.19元、0.63元、3.37元共5份,供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于4元的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,我们经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如某体育品牌的LOGO为![]() ,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
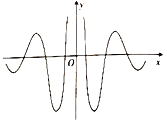
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com