
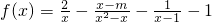
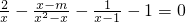 ,
,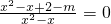 ,
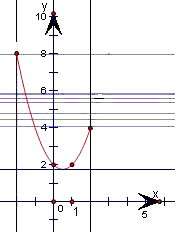
,
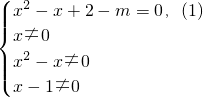
 ;
;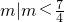 或m=2}
或m=2} 或4≤m<8时,两图象只有一个交点,
或4≤m<8时,两图象只有一个交点,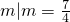 或4≤m<8}.
或4≤m<8}.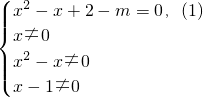 ,欲原方程无实根,考察下面两种情况:①方程(1)无实数根,②方程(1)的实数根为原方程的增根,从而得出答案;
,欲原方程无实根,考察下面两种情况:①方程(1)无实数根,②方程(1)的实数根为原方程的增根,从而得出答案;

科目:高中数学 来源: 题型:
| n |
| 2 |
| n |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本大题共14分)已知函数![]() (
(![]() 为常数),若函数
为常数),若函数![]() 的最大值为
的最大值为![]() .(1)求实数
.(1)求实数![]() 的值;(2)将函数
的值;(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再向下平移2个单位得到函数
个单位,再向下平移2个单位得到函数![]() 的图象,求函数
的图象,求函数![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源:2008年四川省成都市高考数学二模试卷(理科)(解析版) 题型:选择题
 +bx) (a>0且a≠1),则下列叙述正确的是( )
+bx) (a>0且a≠1),则下列叙述正确的是( ) ,b=-1,则函数f(x)为R上的增函数
,b=-1,则函数f(x)为R上的增函数 ,b=-1,则函数f(x)为R上的减函数
,b=-1,则函数f(x)为R上的减函数查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(北京卷解析版) 题型:解答题
已知函数 ,(
,( ),
),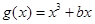
(1)若曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线,求a,b的值
在它们的交点(1,c)处具有公共切线,求a,b的值
(2)当 时,若函数
时,若函数 的单调区间,并求其在区间(-∞,-1)上的最大值。
的单调区间,并求其在区间(-∞,-1)上的最大值。
【解析】(1) ,
,
∵曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线
在它们的交点(1,c)处具有公共切线
∴ ,
,
∴
(2)令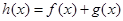 ,当
,当 时,
时,
 令
令 ,得
,得
 时,
时,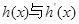 的情况如下:
的情况如下:
|
x |
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
|
|
所以函数 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为
当 ,即
,即 时,函数
时,函数 在区间
在区间 上单调递增,
上单调递增, 在区间
在区间 上的最大值为
上的最大值为 ,
,
当 且
且 ,即
,即 时,函数
时,函数 在区间
在区间 内单调递增,在区间
内单调递增,在区间 上单调递减,
上单调递减, 在区间
在区间 上的最大值为
上的最大值为
当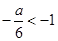 ,即a>6时,函数
,即a>6时,函数 在区间
在区间 内单调递赠,在区间
内单调递赠,在区间 内单调递减,在区间
内单调递减,在区间 上单调递增。又因为
上单调递增。又因为
所以 在区间
在区间 上的最大值为
上的最大值为 。
。
查看答案和解析>>
科目:高中数学 来源:浙江省杭州十四中2010届高三11月月考(理) 题型:解答题
已知函数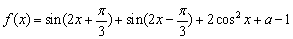 (
( 为常数),若函数
为常数),若函数 的最大值为
的最大值为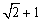 .
.
(1)求实数 的值;
的值;
(2)将函数 的图象向左平移
的图象向左平移 个单位,再向下平移2个单位得到函数
个单位,再向下平移2个单位得到函数 的图象,求函数
的图象,求函数 的单调递减区间.
的单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com