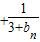【答案】
分析:(1)由a
1=1,2a
n+1=a
n+a
n+2(n∈N
+)可知数列{a
n}是以1为首项的等差数列,设公差为d,由数列递增可知d>0
由a
1,a
2,a
4成等比数可求d,进而可求通项
(2)①(i)当n=1时,b
1≥1=a
1成立
(ii)假设当n=k(k≥1)时成立,即b
k≥a
k=k,由归纳假设证明n=k+1时,b
k+1≥a
k+1②利用b
n+1=b
n2-(n-2)b
n+3,推出
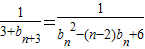
,利用b
n≥n,得到
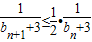
通过放缩与累加,证明出结果.
解答:解:(1)∵a
1=1,2a
n+1=a
n+a
n+2(n∈N
+)
∴数列{a
n}是以1为首项的等差数列,设公差为d,由数列递增可知d>0
∵a
1,a
2,a
4成等比数
∴(1+d)
2=1+3d
∴d=0(舍)或d=1
∴a
n=1+n-1=n
证明:(2)①∵b
n+1=b
n2-(n-2)b
n+3,且b
1≥1,
(i)当n=1时,b
1≥1=a
1成立
(ii)假设当n=k(k≥1)时成立,即b
k≥a
k=k
∴b
k+1≥k+1=a
k+1当n=k+1时,b
k+1=
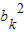
-(k-2)b
k+3,
∴b
k+1-a
k+1=b
k+1-(b
k+1)=
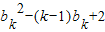
>k
2-k(k-1)+2>0
∴b
k+1≥a
k+1综上可证得,对于任意的正整数n,b
n≥a
n都成立
②∵b
n+1=b
n2-(n-2)b
n+3,∴
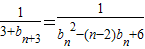
,
b
n2-(n-2)b
n+6=b
n(b
n+2-n)+6≥2b
n+6=2(b
n+3),(∵bn≥n)
∴
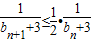
,
∴
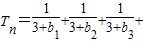
…
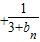
≤
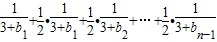
…①
∴
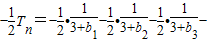
…
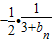
…②,
①+②可得

,
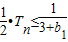
≤

,
∴
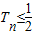
.
∴
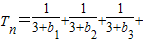
…
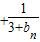
 点评:
点评:本题主要考查了等差中项的应用,等差数列通项公式的求解,数列归纳法在证明数学不等式中的应用,及巧妙的放缩法在不等式的证明中的应用.不能放的太大,也不能缩小的太多.

 …
…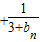 ,证明:
,证明: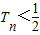 .
.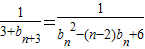 ,利用bn≥n,得到
,利用bn≥n,得到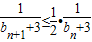
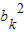 -(k-2)bk+3,
-(k-2)bk+3,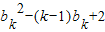 >k2-k(k-1)+2>0
>k2-k(k-1)+2>0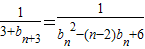 ,
,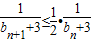 ,
,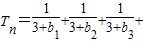 …
…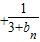 ≤
≤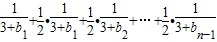 …①
…①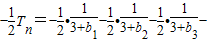 …
…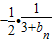 …②,
…②, ,
,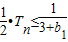 ≤
≤ ,
,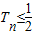 .
.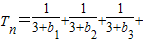 …
…