
| 获取消息渠道 | 看电视 | 收听广播 | 其它渠道 |
| 男性 | 480 | m | 180 |
| 女性 | 384 | 210 | 90 |
| 27 |
| 50 |
| 480+384 |
| 480+384+210+180+90+m |
| 6 |
| 180+90 |
| ||
|
| 4 |
| 5 |
| ||
|
| 1 |
| 15 |
| ||||||
|
| 2 |
| 15 |
| ||||||
|
| 1 |
| 5 |
| 4 |
| 15 |
| 1 |
| 3 |
| X | 2 | 3 | 4 | 5 | 6 | ||||||||||
| P |
|
|
|
|
|
| 14 |
| 3 |


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
| 2 |
| 3 |
| A、3x-15y+4=0 |
| B、15x-3y-2=0 |
| C、15x-3y+2=0 |
| D、3x-y+1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| z |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| AC |
| 1 |
| 2 |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
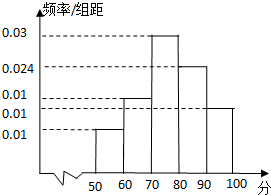 某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.查看答案和解析>>
科目:高中数学 来源: 题型:
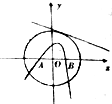 如图⊙O2:x2+y2=9,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A、B两点的抛物线以直线l为准线,则抛物线焦点的轨迹方程是
如图⊙O2:x2+y2=9,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A、B两点的抛物线以直线l为准线,则抛物线焦点的轨迹方程是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com