
设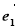 与
与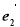 是两个单位向量,其夹角为60°,且
是两个单位向量,其夹角为60°,且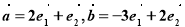 ,
,
(1)求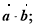
(2)分别求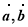 的模;
的模;
(3)求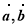 的夹角。
的夹角。
(1) ;(2)
;(2) ;(3)
;(3)
【解析】
试题分析:(1)根据向量的数量积公式和运算律展开,即可求值;
(2) ,然后根据向量的数量积公式展开;
,然后根据向量的数量积公式展开;
(3)根据向量的夹角公式 ,代入前两问的结果,即可求出夹角.
,代入前两问的结果,即可求出夹角.
解:(1)a·b==(2e1+e2)·(-3e1+2e2,)=-6e12+ e1·e2+2e22=- ,(4分)
,(4分)
(2)∵a=2e1+e2,∴|a|2=a2=(2e1+e2)2=4e12+4e1·e2+e22=7,∴|a|= 。(6分)
。(6分)
同理得|b|= 。(8分)
。(8分)
(3)设 的夹角为
的夹角为 。则 cosθ=
。则 cosθ= (7分)
(7分)
= =-
=- , (10分)
, (10分)
∴θ=120°、 (12分)
考点:1.向量的数量积公式;2.运算律;3.模与夹角公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2016届湖南省五市十校高一下学期期中检测数学试卷(解析版) 题型:选择题
设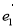 ,
,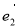 ,
,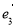 ,
,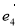 是某平面内的四个单位向量,其中
是某平面内的四个单位向量,其中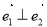 ,
,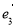 与
与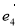 的夹角为45°, 对这个平面内的任意一个向量
的夹角为45°, 对这个平面内的任意一个向量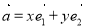 ,规定经过一次“斜二测变换”得到向量
,规定经过一次“斜二测变换”得到向量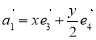 ,设向量
,设向量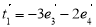 是向量
是向量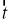 经过一次“斜二测变换”得到的向量,则
经过一次“斜二测变换”得到的向量,则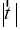 是( )
是( )
A.5 B.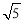 C.73 D.
C.73 D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com