
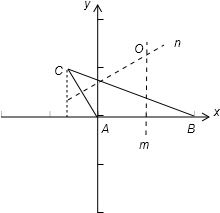
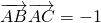 ,若
,若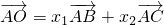 (O是△ABC的外心),则x1+x2的值为________.
(O是△ABC的外心),则x1+x2的值为________.
 ,
, ).
). ,
, ),AC的斜率为-3,∴中垂线n的方程为 y-
),AC的斜率为-3,∴中垂线n的方程为 y- =
= (x+
(x+ ).
). ),由条件
),由条件 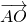 =
=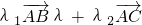 ,
, )=x1 (2,0)+x2 (-
)=x1 (2,0)+x2 (- ,
, )=(2x1-
)=(2x1- x2,
x2, x2 ),
x2 ), x2=1,
x2=1, x2=
x2= ,∴x1 =
,∴x1 = ,x2 =
,x2 = ,∴x1+x2=
,∴x1+x2= ,
, .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com