
【题目】如图,已知圆心坐标为(![]() ,1)的圆M与x轴及直线y=
,1)的圆M与x轴及直线y=![]() x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=
x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=![]() x分别相切于C、D两点.
x分别相切于C、D两点.
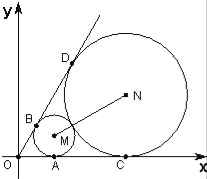
(1)求圆M和圆N的方程;
(2)过点B作直线MN的平行线l,求直线l被圆N截得的弦的长度
【答案】(1)![]() ,
,![]() (2)
(2)![]()
【解析】
试题分析:(1)圆M的圆心已知,且其与x轴及直线![]() 分别相切于A,B两点,故半径易知,另一圆N与圆M外切、且与x轴及直线
分别相切于A,B两点,故半径易知,另一圆N与圆M外切、且与x轴及直线![]() 分别相切于C、D两点,由相似性易得其圆心坐标与半径,依定义写出两圆的方程即可;(2)本题研究的是直线与圆相交的问题,由于B点位置不特殊,故可以由对称性转化为求过A点且与线MN平行的线被圆截得弦的长度,下易解
分别相切于C、D两点,由相似性易得其圆心坐标与半径,依定义写出两圆的方程即可;(2)本题研究的是直线与圆相交的问题,由于B点位置不特殊,故可以由对称性转化为求过A点且与线MN平行的线被圆截得弦的长度,下易解
试题解析:(1)由于⊙M与∠BOA的两边均相切,故M到OA及OB的距离均为⊙M的半
径,则M在∠BOA的平分线上,
同理,N也在∠BOA的平分线上,即O,M,N三点共线,且OMN为∠BOA
的平分线,
∵M的坐标为(![]() ,1),∴M到x轴的距离为1,即⊙M的半径为1,
,1),∴M到x轴的距离为1,即⊙M的半径为1,
则⊙M的方程为![]() ,
,
设⊙N的半径为r,其与x轴的切点为C,连接MA,NC,
由Rt△OAM∽Rt△OCN可知,OM:ON=MA:NC,
即![]() 得r=3,
得r=3,
则OC=![]() ,则⊙N的方程为
,则⊙N的方程为![]() ;
;
(2)由对称性可知,所求的弦长等于过A点直线MN的平行线被⊙N截得的弦的长度,
此弦的方程是![]() ,即:x﹣
,即:x﹣![]() ﹣
﹣![]() =0,
=0,
圆心N到该直线的距离d=![]() ,则弦长=2
,则弦长=2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在如下图象中的两条线段上.该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:
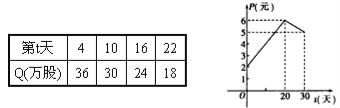
(1)根据提供的图象,写出该种股票每股的交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四面体的下列性质,你认为比较恰当的是 ( )
①各棱长相等,同一顶点上的任意两条棱的夹角都相等;
②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;
③各个面都是全等的正三角形,同一顶点上的任意两条棱的夹角都相等.
A. ① B. ③ C. ①② D. .①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个特定时段内,以点![]() 为中心的
为中心的![]() 海里以内海域被设为警戒水域.点
海里以内海域被设为警戒水域.点![]() 正北
正北![]() 海里有一个雷达观测站
海里有一个雷达观测站![]() ,某时刻测得一艘匀速直线行驶的船只位于点
,某时刻测得一艘匀速直线行驶的船只位于点![]() 北偏东
北偏东![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() ,经过
,经过![]() 分钟又测得该船已行驶到点
分钟又测得该船已行驶到点![]() 北偏东
北偏东![]() (其中
(其中![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() .
.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)是否存在常数![]() ,使得对于定义域内的任意
,使得对于定义域内的任意![]() ,
,![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义在区间
定义在区间![]() 内,对于任意的
内,对于任意的![]() ,有
,有![]() ,且当
,且当![]() 时,
时,![]() .
.
(1)验证函数![]() 是否满足这些条件;
是否满足这些条件;
(2)判断这样的函数是否具有奇偶性和单调性,并加以证明;
(3)若![]() ,求方程
,求方程![]() 的解.
的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com