
【题目】类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四面体的下列性质,你认为比较恰当的是 ( )
①各棱长相等,同一顶点上的任意两条棱的夹角都相等;
②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;
③各个面都是全等的正三角形,同一顶点上的任意两条棱的夹角都相等.
A. ① B. ③ C. ①② D. .①②③
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设命题p:x>0,x-lnx>0,则¬p为
A. x0>0,x0-lnx0>0 B. x0>0,x0-lnx0≤0
C. x>0,x-lnx<0 D. x>0,x-lnx≤0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明“当n为正奇数时,xn+yn能被x+y整除”,第二步归纳假设应写成( )
A.假设n=2k+1(k∈N*)正确,再推n=2k+3正确
B.假设n=2k﹣1(k∈N*)正确,再推n=2k+1正确
C.假设n=k(k∈N*)正确,再推n=k+1正确
D.假设n=k(k≥1)正确,再推n=k+2正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了美化城市环境,某市针对市民乱扔垃圾现象进行罚款处理。为了更好的了解市民的态度,随机抽取了200人进行了调查,得到如下数据:
罚款金额 | 0 | 5 | 10 | 15 | 20 |
会继续乱扔垃圾的人数 | 80 | 50 | 40 | 20 | 10 |
(1)若乱扔垃圾的人数![]() 与罚款金额
与罚款金额![]() 满足线性回归方程,求回归方程
满足线性回归方程,求回归方程![]() ,其中
,其中![]() ,并据此分析,要使乱扔垃圾者不超过
,并据此分析,要使乱扔垃圾者不超过 ,罚款金额至少是多少元?
,罚款金额至少是多少元?
(2)若以调查数据为基础,从5种罚款金额中随机抽取2种不同的数额,求这两种金额之和不低于25元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列结论中正确的是( )
A. 在复平面上,x轴叫做实轴,y轴叫做虚轴 B. 任何两个复数都不能比较大小
C. 如果实数a与纯虚数ai对应,那么实数集与纯虚数集是一一对应的 D. -1的平方根是i
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某企业原有员工1000人,每人每年可为企业创利润15万元,为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超过原有员工的2%,并且每年给每位待岗员工发放生活补贴1万元.据评估,当待岗员工人数![]() 不超过原有员工1.4%时,留岗员工每人每年可为企业多创利润
不超过原有员工1.4%时,留岗员工每人每年可为企业多创利润![]() 万元;当待岗员工人数
万元;当待岗员工人数![]() 超过原有员工1.4%时,留岗员工每人每年可为企业多创利润1.8万元.
超过原有员工1.4%时,留岗员工每人每年可为企业多创利润1.8万元.
(1)求企业年利润![]() (万元)关于待岗员工人数
(万元)关于待岗员工人数![]() 的函数关系式
的函数关系式![]() ;
;
(2)为使企业年利润最大,应安排多少员工待岗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的所有基本事件数为( )
A. 2 B. 3
C. 4 D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆心坐标为(![]() ,1)的圆M与x轴及直线y=
,1)的圆M与x轴及直线y=![]() x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=
x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=![]() x分别相切于C、D两点.
x分别相切于C、D两点.
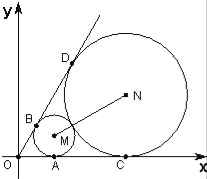
(1)求圆M和圆N的方程;
(2)过点B作直线MN的平行线l,求直线l被圆N截得的弦的长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的新产品必须先靠广告打开销路,该产品广告效应![]() (单位:元)是产品的销售额与广告费
(单位:元)是产品的销售额与广告费![]() (单位:元)之间的差,如果销售额与广告费
(单位:元)之间的差,如果销售额与广告费![]() 的算术平方根成正比,根据对市场的抽样调查,每付出100元的广告费,所得销售额是1000元.
的算术平方根成正比,根据对市场的抽样调查,每付出100元的广告费,所得销售额是1000元.
(Ⅰ)求出广告效应![]() 与广告费
与广告费![]() 之间的函数关系式;
之间的函数关系式;
(Ⅱ)该企业投入多少广告费才能获得最大的广告效应?是不是广告费投入越多越好?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com