
【题目】在一个特定时段内,以点![]() 为中心的
为中心的![]() 海里以内海域被设为警戒水域.点
海里以内海域被设为警戒水域.点![]() 正北
正北![]() 海里有一个雷达观测站
海里有一个雷达观测站![]() ,某时刻测得一艘匀速直线行驶的船只位于点
,某时刻测得一艘匀速直线行驶的船只位于点![]() 北偏东
北偏东![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() ,经过
,经过![]() 分钟又测得该船已行驶到点
分钟又测得该船已行驶到点![]() 北偏东
北偏东![]() (其中
(其中![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() .
.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.
【答案】(1)![]() (海里/小时);(2)船会进入警戒水域,理由见解析.
(海里/小时);(2)船会进入警戒水域,理由见解析.
【解析】
试题分析:(1)先根据题意画出简图确定![]() 的值,根据
的值,根据![]() 球场
球场![]() 的余弦值,再由余弦定理求出
的余弦值,再由余弦定理求出![]() 的值,从而可得到船的行驶速度;(2)设直线
的值,从而可得到船的行驶速度;(2)设直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .根据余弦定理求出
.根据余弦定理求出![]() 的值,进而可得到其正弦值,再由正弦定理可得
的值,进而可得到其正弦值,再由正弦定理可得![]() 的长度,从而可确定
的长度,从而可确定![]() 在点
在点![]() 和点
和点![]() 之间,根据
之间,根据![]() 求出
求出![]() 的长度,然后过点
的长度,然后过点![]() 作
作![]() ,则
,则![]() 为点
为点![]() 到直线
到直线![]() 的距离,进而在
的距离,进而在![]() 中求出
中求出![]() 的值,进行比较可得得到答案.
的值,进行比较可得得到答案.
试题解析:(1)如图,![]()
![]() ,
,
由于![]() ,所以
,所以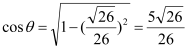 .
.
由余弦定理得![]() ,
,
所以船的行驶速度为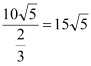 (海里/小时).
(海里/小时).
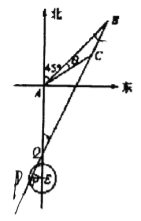
(2)如图所示,设直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .在
.在![]() 中,
中,
由余弦定理得,![]() ,
,
从而![]() .
.
在![]() 中,由正弦定理得,
中,由正弦定理得,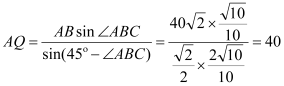 ,
,
由于![]() ,所以点
,所以点![]() 位于点
位于点![]() 和点
和点![]() 之间,且
之间,且![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 为点
为点![]() 到直线
到直线![]() 的距离.
的距离.
在![]() 中,
中,![]() ,
,
所以船会进入警戒水域.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-![]() .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了美化城市环境,某市针对市民乱扔垃圾现象进行罚款处理。为了更好的了解市民的态度,随机抽取了200人进行了调查,得到如下数据:
罚款金额 | 0 | 5 | 10 | 15 | 20 |
会继续乱扔垃圾的人数 | 80 | 50 | 40 | 20 | 10 |
(1)若乱扔垃圾的人数![]() 与罚款金额
与罚款金额![]() 满足线性回归方程,求回归方程
满足线性回归方程,求回归方程![]() ,其中
,其中![]() ,并据此分析,要使乱扔垃圾者不超过
,并据此分析,要使乱扔垃圾者不超过 ,罚款金额至少是多少元?
,罚款金额至少是多少元?
(2)若以调查数据为基础,从5种罚款金额中随机抽取2种不同的数额,求这两种金额之和不低于25元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某企业原有员工1000人,每人每年可为企业创利润15万元,为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超过原有员工的2%,并且每年给每位待岗员工发放生活补贴1万元.据评估,当待岗员工人数![]() 不超过原有员工1.4%时,留岗员工每人每年可为企业多创利润
不超过原有员工1.4%时,留岗员工每人每年可为企业多创利润![]() 万元;当待岗员工人数
万元;当待岗员工人数![]() 超过原有员工1.4%时,留岗员工每人每年可为企业多创利润1.8万元.
超过原有员工1.4%时,留岗员工每人每年可为企业多创利润1.8万元.
(1)求企业年利润![]() (万元)关于待岗员工人数
(万元)关于待岗员工人数![]() 的函数关系式
的函数关系式![]() ;
;
(2)为使企业年利润最大,应安排多少员工待岗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的所有基本事件数为( )
A. 2 B. 3
C. 4 D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B={抽到二等品},事件C={抽到三等品},且已知P(A)=0.65,P(B)=0.2,P(C)=0.1.则事件“抽到的是二等品或三等品”的概率为( )
A. 0.7 B. 0.65
C. 0.35 D. 0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆心坐标为(![]() ,1)的圆M与x轴及直线y=
,1)的圆M与x轴及直线y=![]() x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=
x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=![]() x分别相切于C、D两点.
x分别相切于C、D两点.
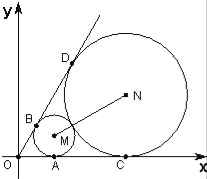
(1)求圆M和圆N的方程;
(2)过点B作直线MN的平行线l,求直线l被圆N截得的弦的长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】销售甲、乙两种商品所得利润分别是![]() 万元,它们与投入资金
万元,它们与投入资金![]() 万元的关系分别为
万元的关系分别为![]() (其中
(其中![]() 都为常数),函数
都为常数),函数![]() 对应的曲线
对应的曲线![]() 如图所示.
如图所示.
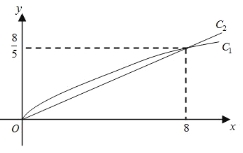
(1)求函数![]() 的解析式;
的解析式;
(2)若该商场一共投资8万元经销甲、乙两种商品,求该商场所获利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生作了一次调查,所得数据如表:
认为作业多 | 认为作业不多 | 总计 | |
喜欢玩电脑游戏 | 18 | 9 | 27 |
不喜欢玩电脑游戏 | 8 | 15 | 23 |
总计 | 26 | 24 | 50 |
由表中数据计算得到K2的观测值k≈5.059,于是________(填“能”或“不能”)在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com