Question

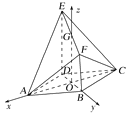
【题目】在如图所示的几何体中，四边形是边长为2的菱形，平面，， ．

（1）证明：平面平面；

（2）求二面角的余弦值．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

（1）连接交于点，证明，，推出平面，得到平面平面；

（2）取的中点，连接，则，说明两两垂直，以所在直线分别作为轴，轴，轴建立空间直角坐标系，求出平面的一个法向量，平面的一个法向量，用向量夹角公式求出向量夹角余弦值，即可得出结果.

（1）连接交于点，因为是菱形，

所以，

∵平面，∴，

又平面，平面，，

∴平面，

∴平面ACF⊥平面BDEF．

（2）取的中点，连接，则，

∵平面，∴平面，∴两两垂直．

以所在直线分别作为轴，轴，轴建立空间直角坐标系（如图），

则，，，，，

，，，

，,

则，，

所以，，且，

所以平面，

所以平面的一个法向量为．

设平面的一个法向量为，

则，∴，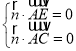

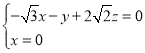得，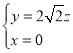

令，

得平面的一个法向量，

从而.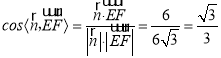

即二面角的余弦值.