Question

6．已知△ABC中，C=2B，若∠BAC的平分线把△ABC的面积分成$\sqrt{3}$：1两部分，则A=90°．

Answer 1

分析 如图，AD是∠BAC的平分线．由两三角形的面积比为$\sqrt{3}$：1可得相应的边长之比，利用正弦定理可得正弦之比，然后转化为角B的关系式，由特殊角的三角函数值得到B=30°，则C=60°，由三角形内角和定理得到A的度数．

解答 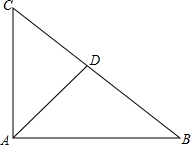解：由题意可得，S_△ABD：S_△ACD=$\sqrt{3}$：1，BD：CD=$\sqrt{3}$：1，
由正弦定理得，$\frac{AD}{sinC}$=$\frac{CD}{sin\frac{A}{2}}$，$\frac{AD}{sinB}$=$\frac{BD}{sin\frac{A}{2}}$，
所以$\frac{sinC}{sinB}$=$\frac{BD}{CD}$=$\frac{\sqrt{3}}{1}$=$\sqrt{3}$，即$\frac{2sinBcosB}{sinB}$=$\sqrt{3}$，
所以cosB=$\frac{\sqrt{3}}{2}$，
因为0＜B＜π，
所以B=30°，
所以C=2B=60°
所以A=90°，
故答案为：90°．

点评 本题考查正弦定理的应用、三角函数中的恒等变换，考查学生分析解决问题的能力．