
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线C的极坐标方程为
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求直线![]() 和曲线C的直角坐标方程;
和曲线C的直角坐标方程;
(2)若点P为曲线C上任一点,求点P到直线![]() 的距离的最大值,并求此时点P的坐标.
的距离的最大值,并求此时点P的坐标.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 在统计学中,回归分析是检验两个分类变量是否有关系的一种统计方法
B. 线性回归方程对应的直线![]() 至少经过其样本数据点中的
至少经过其样本数据点中的![]() ,
,![]() ,
,![]()
![]() 一个点
一个点
C. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D. 在回归分析中,相关指数![]() 为
为![]() 的模型比相关指数
的模型比相关指数![]() 为
为![]() 的模型拟合的效果差
的模型拟合的效果差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】禽流感一直在威胁我们的生活,某疾病控制中心为了研究禽流感病毒繁殖个数![]() (个)随时间
(个)随时间![]() (天)变化的规律,收集数据如下:
(天)变化的规律,收集数据如下:
天数 | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数 | 6 | 12 | 25 | 49 | 95 | 190 |
作出散点图可看出样本点分布在一条指数型函数![]() 的周围.
的周围.
保留小数点后两位数的参考数据:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]()
(1)求出![]() 关于
关于![]() 的回归方程(保留小数点后两位数字);
的回归方程(保留小数点后两位数字);
(2)已知![]() ,估算第四天的残差.
,估算第四天的残差.
参考公式: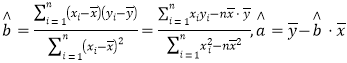
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,沿
,沿![]() 将四边形
将四边形![]() 折起,连接
折起,连接![]() .
.
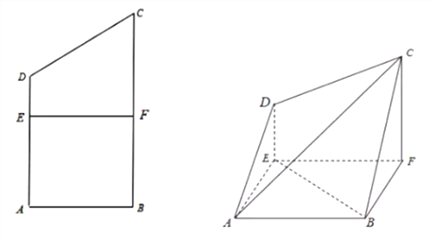
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() .
.
(I)求二面角![]() 的平面角的大小;
的平面角的大小;
(II)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,如果存在常数p,使得对任意正整数n,总有
,如果存在常数p,使得对任意正整数n,总有![]() 成立,那么我们称数列
成立,那么我们称数列![]() 为“p-摆动数列”.
为“p-摆动数列”.
(Ⅰ)设![]() ,
,![]() ,
,![]() ,判断
,判断![]() 、
、![]() 是否为“p-摆动数列”,并说明理由;
是否为“p-摆动数列”,并说明理由;
(Ⅱ)已知“p-摆动数列”![]() 满足
满足![]() ,
,![]() ,求常数p的值;
,求常数p的值;
(Ⅲ)设![]() ,且数列
,且数列![]() 的前n项和为
的前n项和为![]() ,求证:数列
,求证:数列![]() 是“p-摆动数列”,并求出常数p的取值范围.
是“p-摆动数列”,并求出常数p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 、
、![]() 、
、![]() ,且
,且![]() 都有
都有![]() ,满足
,满足![]() 的实数
的实数![]() 有且只有
有且只有![]() 个,给出下述四个结论:
个,给出下述四个结论:
①满足题目条件的实数![]() 有且只有
有且只有![]() 个;②满足题目条件的实数
个;②满足题目条件的实数![]() 有且只有
有且只有![]() 个;
个;
③![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的取值范围是
的取值范围是![]() .
.
其中所有正确结论的编号是( )
A.①④B.②③C.①②③D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划销售某种食品,现邀请甲、乙两个商家进场试销10天.两个商家向超市提供的日返利方案如下:甲商家每天固定返利60元,且每卖出一件食品商家再返利3元;乙商家无固定返利,卖出不超出30件(含30件)的食品,每件食品商家返利5元,超出30件的部分每件返利10元. 经统计,试销这10天两个商家每天的销量如图所示的茎叶图(茎为十位数字,叶为个位数字):
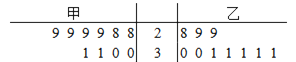
(1)现从甲商家试销的10天中随机抽取两天,求这两天的销售量都小于30件的概率;
(2)根据试销10天的数据,将频率视作概率,用样本估计总体,回答以下问题:
①记商家乙的日返利额为X(单位:元),求X的分布列和数学期望;
②超市拟在甲、乙两个商家中选择一家长期销售,如果仅从日返利额的数学期望考虑,请利用所学的统计学知识为超市作出选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com