
【题目】已知函数f(x)=log4(4x+1)+kx,(k∈R)为偶函数.
(1)求k的值;
(2)若方程f(x)=log4(a2x﹣a)有且只有一个根,求实数a的取值范围.
【答案】解:(I) 由题意得f(﹣x)=f(x),
即![]() ,
,
化简得![]() =2kx,
=2kx,
从而4(2k+1)x=1,此式在x∈R上恒成立,
∴k=-![]()
(II)由题意,原方程化为![]() 且a2x﹣a>0
且a2x﹣a>0
即:令2x=t>0![]()
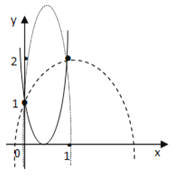
函数y=(1﹣a)t2+at+1的图象过定点(0,1),(1,2)如图所示:
若方程(1)仅有一正根,只有如图的三种情况,
可见:a>1,即二次函数y=(1﹣a)t2+at+1的
开口向下都可,且该正根都大于1,满足不等式(2),
当二次函数y=(1﹣a)t2+at+1的开口向上,
只能是与x轴相切的时候,
此时a<1且△=0,即a=-2-2![]() 也满足不等式(2)
也满足不等式(2)
综上:a>1或a=-2-2![]()
【解析】(Ⅰ)根据偶函数可知f(x)=f(﹣x),取x=﹣1代入即可求出k的值;
(Ⅱ)根据方程![]() 有且只有一个实根,化简可得
有且只有一个实根,化简可得![]() 有且只有一个实根,令t=2x>0,则转化成新方程有且只有一个正根,结合函数的图象讨论a的取值,即可求出实数a的取值范围.
有且只有一个实根,令t=2x>0,则转化成新方程有且只有一个正根,结合函数的图象讨论a的取值,即可求出实数a的取值范围.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,
, ![]() 是坐标原点,
是坐标原点, ![]() 分别为其左右焦点,
分别为其左右焦点, ![]() ,
, ![]() 是椭圆上一点,
是椭圆上一点, ![]() 的最大值为
的最大值为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]()
(i)求证: ![]() 为定值;
为定值;
(ii)求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a为实数,p:点M(1,1)在圆(x+a)2+(y﹣a)2=4的内部; q:x∈R,都有x2+ax+1≥0.
(1)若p为真命题,求a的取值范围;
(2)若q为假命题,求a的取值范围;
(3)若“p且q”为假命题,且“p或q”为真命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2![]() sin(ax﹣
sin(ax﹣![]() )cos(ax﹣
)cos(ax﹣![]() )+2cos2(ax﹣
)+2cos2(ax﹣![]() )(a>0),且函数的最小正周期为
)(a>0),且函数的最小正周期为![]() .
.
(Ⅰ)求a的值;
(Ⅱ)求f(x)在[0,![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=3,若a,b∈[﹣1,1],a+b≠0时,有![]() >0成立.
>0成立.
(1)判断f(x)在[﹣1,1]上的单调性,并证明;
(2)解不等式:f(x+![]() )<f(
)<f(![]() );
);
(3)若当a∈[﹣1,1]时,f(x)≤m2﹣2am+3对所有的x∈[﹣1,1]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线y2=2px(p>0)的焦点,斜率为2![]() 的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若![]() =
=![]() +λ
+λ![]() , 求λ的值.
, 求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求下列曲线的标准方程:
(1)与椭圆![]() +
+![]() =1有相同的焦点,直线y=
=1有相同的焦点,直线y=![]() x为一条渐近线.求双曲线C的方程.
x为一条渐近线.求双曲线C的方程.
(2)焦点在直线3x﹣4y﹣12=0 的抛物线的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段,下表是初赛成绩(得分均为整数,满分为100分)的频率分布表.
分组(分数段) | 频数(人数) | 频率 |
|
| 0.16 |
| 17 |
|
| 19 | 0.38 |
|
|
|
合计 | 50 | 1 |
(Ⅰ)求频率分布表中![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)决赛规则如下:参加决赛的每位同学依次口答3道判断题,答对3道题获得一等奖,答对2道题获得二等奖,答对1道题获得三等奖,否则不得奖.若某同学进入决赛,且其每次答题回答正确与否均是等可能的,试列出他回答问题的所有可能情况,并求出他至少获得二等奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com