
【题目】已知过抛物线y2=2px(p>0)的焦点,斜率为2![]() 的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若![]() =
=![]() +λ
+λ![]() , 求λ的值.
, 求λ的值.
【答案】解:(1)直线AB的方程是y=2![]() (x﹣
(x﹣![]() ),与y2=2px联立,有4x2﹣5px+p2=0,
),与y2=2px联立,有4x2﹣5px+p2=0,
∴x1+x2=![]()
由抛物线定义得:|AB|=x1+x2+p=9
∴p=4,∴抛物线方程是y2=8x.
(2)由p=4,4x2﹣5px+p2=0得:x2﹣5x+4=0,
∴x1=1,x2=4,
y1=﹣2![]() ,y2=4
,y2=4![]() ,从而A(1,﹣2
,从而A(1,﹣2![]() ),B(4,4
),B(4,4![]() ).
).
设![]() =(x3 , y3)=(1,﹣2
=(x3 , y3)=(1,﹣2![]() )+λ(4,4
)+λ(4,4![]() )=(4λ+1,4
)=(4λ+1,4![]() λ﹣2
λ﹣2![]() )
)
又[2![]() (2λ﹣1)]2=8(4λ+1),解得:λ=0,或λ=2.
(2λ﹣1)]2=8(4λ+1),解得:λ=0,或λ=2.
【解析】(1)直线AB的方程与y2=2px联立,有4x2﹣5px+p2=0,从而x1+x2=![]() , 再由抛物线定义得:|AB|=x1+x2+p=9,求得p,则抛物线方程可得.
, 再由抛物线定义得:|AB|=x1+x2+p=9,求得p,则抛物线方程可得.
(2)由p=4,4x2﹣5px+p2=0求得A(1,﹣2![]() ),B(4,4
),B(4,4![]() ).再求得设
).再求得设![]() 的坐标,最后代入抛物线方程即可解得λ.
的坐标,最后代入抛物线方程即可解得λ.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】设x,y,a∈R* , 且当x+2y=1时, ![]() +
+ ![]() 的最小值为6
的最小值为6 ![]() ,则当
,则当 ![]() +
+ ![]() =1时,3x+ay的最小值是( )
=1时,3x+ay的最小值是( )
A.6 ![]()
B.6
C.12
D.12 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数y=|x|与函数y=( ![]() )2表示同一个函数;
)2表示同一个函数;
②奇函数的图象一定通过直角坐标系的原点;
③若函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4];
④设函数f(x)是在区间[a,b]上图象连续的函数,且f(a)f(b)<0,则方程f(x)=0在区间[a,b]上至少有一实根;
其中正确命题的序号是(填上所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx,(k∈R)为偶函数.
(1)求k的值;
(2)若方程f(x)=log4(a2x﹣a)有且只有一个根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x , f(a+2)=27,函数g(x)=λ2ax﹣4x的定义域为[0,2].
(1)求a的值;
(2)若λ=2,试判断函数g(x)在[0,2]上的单调性,并加以证明;
(3)若函数g(x)的最大值是 ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D﹣ABC中,已知△BCD是正三角形,平面ABC⊥平面BCD,AB=BC=a,AC= ![]() a,E为BC的中点,F在棱AC上,且AF=3FC.
a,E为BC的中点,F在棱AC上,且AF=3FC. 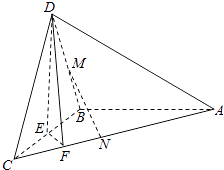
(1)求三棱锥D﹣ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN= ![]() CA,求证:MN∥平面DEF.
CA,求证:MN∥平面DEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com