
【题目】如图,己知抛物线![]() ,直线
,直线![]() 交抛物线于
交抛物线于![]() 两点,
两点,![]() 是抛物线外一点,连接
是抛物线外一点,连接![]() 分别交地物线于点
分别交地物线于点![]() ,且
,且![]() .
.

(1)若![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
(2)若![]() ,且
,且![]() 平行x轴,求
平行x轴,求![]() 面积.
面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设![]() ,根据向量关系可用
,根据向量关系可用![]() 的坐标表示
的坐标表示![]() 的坐标,利用
的坐标,利用![]() 在抛物线可得
在抛物线可得![]() 的坐标满足的方程,同理利用D在抛物线也可得
的坐标满足的方程,同理利用D在抛物线也可得![]() 的坐标满足的方程,联立直线方程和抛物线方程结合韦达定理可得
的坐标满足的方程,联立直线方程和抛物线方程结合韦达定理可得![]() 的横坐标为2.也可以利用
的横坐标为2.也可以利用![]() 在抛物线上及
在抛物线上及![]() 得到
得到![]() ,利用
,利用![]() 、
、![]() 的中点、
的中点、![]() 的中点共线得到
的中点共线得到![]() 的横坐标为2.
的横坐标为2.
(2)根据(1)的相关结果可用![]() 表示
表示![]() 的坐标、
的坐标、![]() 的坐标及
的坐标及![]() 中点
中点![]() 的坐标,根据
的坐标,根据![]() 在抛物线上可得
在抛物线上可得![]() 的值并求出
的值并求出![]() 的坐标,最后利用公式
的坐标,最后利用公式![]() 可求面积.
可求面积.
(1)解法1:![]() ,设
,设![]() ,
,
则![]() ,由
,由![]() 可得
可得
![]() ,故
,故![]() ,同理
,同理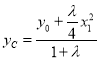 ,
,
故 ,代入抛物线得:
,代入抛物线得: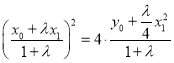 ,
,
化简得:![]() ,
,
同理得:![]() ,
,
所以![]() 为方程
为方程![]() 的两根,
的两根,
又由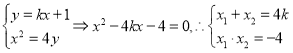 ,
,
将![]() 代入
代入![]() 且
且![]() ①,
①,
将![]() 代入①,得
代入①,得![]() ,故
,故![]() .
.
故点P的轨迹方程为![]() .
.
解法2:同解法1知![]()
![]() ,
,
设线段![]() 的中点分别为
的中点分别为![]() ,易知
,易知![]() 三点共线,
三点共线,
![]() (
(![]() 为实数),所以
为实数),所以![]() .
.
以下同解法1.
(2)由![]() 为方程
为方程![]() 的两根,
的两根,
可得:![]() .
.
由(1)得![]() ,因为
,因为![]() ,所以
,所以![]() ,故
,故![]() .
.
![]() 轴且
轴且![]() 在抛物线上,∴
在抛物线上,∴![]() 关于
关于![]() 轴对称.
轴对称.
![]() ,
,![]() 及
及![]() ,
,
 且
且![]() .
.
∵![]() 在抛物线上,
在抛物线上,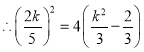 ,解得
,解得![]() .
.
设![]() 的中点为
的中点为![]() ,则
,则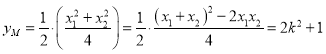 ,
,
所以![]() ,
,
而![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则下列命题正确的是______
,则下列命题正确的是______![]() 填上你认为正确的所有命题的序号
填上你认为正确的所有命题的序号![]()
![]() 函数
函数![]() 的单调递增区间是
的单调递增区间是![]() ;
;![]() 函数
函数![]() 的图像关于点
的图像关于点![]() 对称;
对称;
![]() 函数
函数![]() 的图像向左平移
的图像向左平移![]() 个单位长度后,所得的图像关于y轴对称,则m的最小值是
个单位长度后,所得的图像关于y轴对称,则m的最小值是![]() ;
;
![]() 若实数m使得方程
若实数m使得方程![]() 在
在![]() 上恰好有三个实数解
上恰好有三个实数解![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一次全市高中男生身高统计调查数据显示:全市10万名男生的身高服从正态分布![]() .现从某学校高中男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和190cm之间,将身高的测量结果按如下方式分成5组:第1组[160,166),第2组[166,172),...,第5组[184,190]下表是按上述分组方法得到的频率分布表:
.现从某学校高中男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和190cm之间,将身高的测量结果按如下方式分成5组:第1组[160,166),第2组[166,172),...,第5组[184,190]下表是按上述分组方法得到的频率分布表:
分组 | [160,166) | [166,172) | [172,178) | [178,184) | [184,190] |
人数 | 3 | 10 | 24 | 10 | 3 |
这50个数据的平均数和方差分别比10万个数据的平均数和方差多1和6.68,且这50个数据的方差为![]() .(同组中的身高数据用该组区间的中点值作代表):
.(同组中的身高数据用该组区间的中点值作代表):
(1)求![]() ,
,![]() ;
;
(2)给出正态分布的数据:![]() ,
,![]() .
.
(i)若从这10万名学生中随机抽取1名,求该学生身高在(169,179)的概率;
(ii)若从这10万名学生中随机抽取1万名,记![]() 为这1万名学生中身高在(169,184)的人数,求
为这1万名学生中身高在(169,184)的人数,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场对职工开展了安全知识竞赛的活动,将竞赛成绩按照![]() ,
,![]() ,… ,
,… ,![]() 分成
分成![]() 组,得到下面频率分布直方图.根据频率分布直方图.下列说法正确的是( )
组,得到下面频率分布直方图.根据频率分布直方图.下列说法正确的是( )
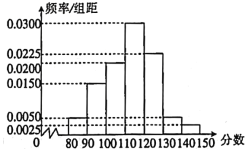
①根据频率分布直方图估计该商场的职工的安全知识竞赛的成绩的众数估计值为![]() ;
;
②根据频率分布直方图估计该商场的职工的安全知识竞赛的成绩的中位数约为![]() ;
;
③若该商场有![]() 名职工,考试成绩在
名职工,考试成绩在![]() 分以下的被解雇,则解雇的职工有
分以下的被解雇,则解雇的职工有![]() 人;
人;
④若该商场有![]() 名职工,商场规定只有安全知识竞赛超过
名职工,商场规定只有安全知识竞赛超过![]() 分(包括
分(包括![]() 分)的人员才能成为安全科成员,则安全科成员有
分)的人员才能成为安全科成员,则安全科成员有![]() 人.
人.
A.①③B.②③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交![]() 元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足
元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足![]() 升的,按
升的,按![]() 升计算(如剩余
升计算(如剩余![]() 升,记为剩余
升,记为剩余![]() 升).例如:结账时,某桌剩余酒量恰好为
升).例如:结账时,某桌剩余酒量恰好为![]() 升,则该桌的每位客人还应付
升,则该桌的每位客人还应付![]() 元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的
元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的![]() 组数据
组数据![]() (其中
(其中![]() 表示饮酒人数,
表示饮酒人数,![]() (升)表示饮酒量):
(升)表示饮酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
剩余酒量(单位:升) |
|
|
|
|
|
结账时的倍率 |
|
|
|
|
|
(1)求由这![]() 组数据得到的
组数据得到的![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)小王约了![]() 位朋友坐在一桌饮酒,小王及朋友用量杯共量取了
位朋友坐在一桌饮酒,小王及朋友用量杯共量取了![]() 升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请
升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请![]() 位或
位或![]() 位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
参考数据:回归直线的方程是![]() ,其中
,其中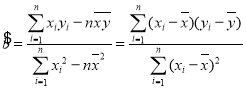 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,且当
的奇函数,且当![]() 时,
时,![]() ,其中
,其中![]() 是常数.
是常数.
(1)求![]() 的解析式;
的解析式;
(2)求实数![]() 的值,使得函数
的值,使得函数![]() ,
,![]() 的最小值为
的最小值为![]() ;
;
(3)已知函数![]() 满足:对任何不小于
满足:对任何不小于![]() 的实数
的实数![]() ,都有
,都有![]() ,其中
,其中![]() 为不小于
为不小于![]() 的正整数常数,求证:
的正整数常数,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com