
����Ŀ��������ѧ��һ����ѧ��ȤС���У���λͬѧ�Ų�Դ�������������ֱ��ɯʿ���ǡ�����Ͳ�ѩ����λ������ѡ����һλ�����Ը��о�����������ѡ������Ҹ�����ͬ����λͬѧһ������ͼ�����Ա����ʦ��������ʦ�²��������˸��Ե��о���������ʦ�������仰�������Ų�Դ�о�����ɯʿ���ǣ���������о��Ŀ϶����Dz�ѩ�ۣ��۸�����Ȼ�����о�ɯʿ���ǣ����ܿ�ϧ������ʦ�����ֲ·���ֻ�¶���һ�䣮�ݴ˿�����֪�Ų�Դ�������������ֱ��о�����__________����Aɯʿ���ǡ�B�����C��ѩ�ۣ���˳����д��ĸ���ɣ���
���𰸡�![]()
���������⣺������ʦ�¶Ե��Ǣ٣���
���Ų�Դ�о�����ɯʿ���ǣ�
��������о��IJ�һ���Dz�ѩ�ۣ�
�۸����о�����ɯʿ���ǣ�
�٢�ì�ܣ��������
������ʦ�¶Ե���������
���Ų�Դ�о��IJ���ɯʿ���ǣ�
��������о��Ŀ϶����Dz�ѩ�ۣ�
�۸����о�����ɯʿ���ǣ�
���Ų�Դ�о��IJ��Dz�ѩ�ۣ�������о���������������о�����ɯʿ���ǣ�
�������⣻
������ʦ�¶Ե��Ǣۣ���
���Ų�Դ�о��IJ���ɯʿ���ǣ�
��������о��IJ�һ���Dz�ѩ�ۣ�
�۸�����Ȼ�����о�ɯʿ���ǣ�
�ݴ˿�֪��������о�����ɯʿ���ǣ����������о�����˭��ȷ����
�ų����ֿ���.
�ݴ˿�����֪�Ų�Դ�������������ֱ��о�����![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ǡ�ABC�У�a��b��c�ֱ�Ϊ��A��B��C���Եıߣ��� ![]() =2csinA
=2csinA
��1��ȷ����C�Ĵ�С��
��2����c= ![]() ���ҡ�ABC�����Ϊ
���ҡ�ABC�����Ϊ ![]() ����a+b��ֵ��
����a+b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ����
����![]() ������
������![]() ��ֱ�����Σ�
��ֱ�����Σ�![]() ,
,![]() ��
��![]() �ϵĵ�.
�ϵĵ�.
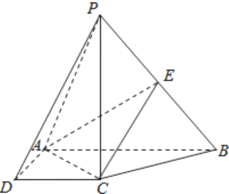
��1����֤: ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��
��![]() ���е㣬�Ҷ����
���е㣬�Ҷ����![]() ������ֵΪ
������ֵΪ![]() ����ֱ��
����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Ź�˾Ϊ�˻�ø�������棬�����Ժ�ÿ��Ͷ��һ���ʽ����ڹ������������г����飬ÿ��Ͷ�����t����Ԫ�����������۶�Լ��2t+ ![]() ��
�� ![]() ������Ԫ��t��0����
������Ԫ��t��0����
��1������˾�����������治����1.5����Ԫ����ÿ��Ͷ�Ź������ٶ��ٰ���Ԫ��
��2���ֹ�˾��Ͷ��6����Ԫ�ֱ����ڵ�����Ѻ��²�Ʒ��������Ԥ�⣬ÿͶ���²�Ʒ������x����Ԫ�����������۶�Լ�� ![]() +3x+
+3x+ ![]() ������Ԫ������η�������ʽ�ʹ�ù�˾����������������������=�������۶Ͷ�룩
������Ԫ������η�������ʽ�ʹ�ù�˾����������������������=�������۶Ͷ�룩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У��ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c����֪2ccosA+a=2b
��1�����C��ֵ��
��2����c=2���ҡ�ABC�����Ϊ ![]() ����a��b��
����a��b��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]()
![]() ��
��
������ֱ��![]()
![]() ������
������![]() ��
��![]() �ֱ���
�ֱ���![]() ����.������
����.������
![]() �ڵ�
�ڵ�![]() ��������Ϊ
��������Ϊ![]() ��
�� ![]() �ڵ�
�ڵ�![]() ��������Ϊ
��������Ϊ![]() .
.
��������![]() ʱ����
ʱ����![]()
![]() ����
����![]() ��ֵ��
��ֵ��
��������![]() ����
����![]() �����ֵ��
�����ֵ��
�����躯��![]() ���䶨������ǡ��������ͬ�ļ�ֵ��
���䶨������ǡ��������ͬ�ļ�ֵ��![]() ��
�� ![]() ����
����![]() ��
��
��![]() ����
����![]() ���������
���������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a=��2 ![]() sin��x+
sin��x+ ![]() ��dx�������ʽ��x2+
��dx�������ʽ��x2+ ![]() ��5��չ��ʽ��x��ϵ����չ��ʽ�и���ϵ��֮�ͣ�
��5��չ��ʽ��x��ϵ����չ��ʽ�и���ϵ��֮�ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�ֱ�����ABC�������ڽ�A��B��C���Եıߣ������㣨2b��a��cosC=ccosA��
���������C�Ĵ�С��
��������![]() ����y�����ֵ���жϵ�yȡ�����ֵʱ��ABC����״��
����y�����ֵ���жϵ�yȡ�����ֵʱ��ABC����״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2��kx+��2k��3����
��1����k= ![]() ʱ���ⲻ��ʽf��x����0��
ʱ���ⲻ��ʽf��x����0��
��2����f��x����0������x��R���������ʵ��k��ȡֵ��Χ��
��3��������f��x��������ͬ���������� ![]() ����ʵ��k��ȡֵ��Χ��
����ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com