
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用倍角公式化简,然后逐一核对四个命题得答案.
解答 解:f(x)=2sinxcosx+2=sin2x+2.
当x∈($\frac{π}{4}$,$\frac{π}{2}$)时,2x∈($\frac{π}{2},π$),∴f(x)在($\frac{π}{4}$,$\frac{π}{2}$)上是递减的,故①错误;
∵f(0)=sin0+2=2,∴f(x)的图象不关于原点对称,故②错误;
由T=$\frac{2π}{2}=π$,可得f(x)的最小正周期为π,故③错误;
f(x)=2sinxcosx+2=sin2x+2 的最大值为3,故④正确.
∴正确选项的个数是1个.
故选:A.
点评 本题考查命题的真假判断与应用,考查了y=Asin(ωx+φ)型函数的图象和性质,是中档题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 1或-$\frac{1}{2}$ | D. | -1或-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
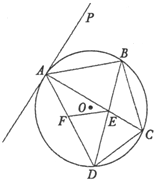 已知如图,四边形ABCD是圆O的内接四边形,对角线AC,BD交于点E,直线AP是圆O的切线,切点为A,∠PAB=∠BAC.
已知如图,四边形ABCD是圆O的内接四边形,对角线AC,BD交于点E,直线AP是圆O的切线,切点为A,∠PAB=∠BAC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
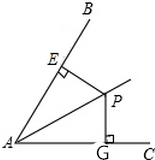 如图,点P是∠BAC内一点,且P到AB、AC的距离PE=PG,则下列哪一个能作为△PEA≌△PGA的理由( )
如图,点P是∠BAC内一点,且P到AB、AC的距离PE=PG,则下列哪一个能作为△PEA≌△PGA的理由( )| A. | HL | B. | AAS | C. | SSS | D. | ASA |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com