
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 由已知函数解析式求出y=f(x-1)的解析式,结合函数f(x)为奇函数,作出函数图象,数形结合可得函数$y=f(x-1)-\frac{1}{2}(x-1)$的零点个数.
解答 解:由$f(x)=\left\{\begin{array}{l}{(x+2)^{2}-1,x<-1}\\{0,-1≤x≤0}\end{array}\right.$,得
$f(x-1)=\left\{\begin{array}{l}{(x+1)^{2}-1,x<0}\\{0,0≤x≤1}\end{array}\right.$,
函数$y=f(x-1)-\frac{1}{2}(x-1)$的零点,即方程f(x-1)-$\frac{1}{2}(x-1)$的根,
也就是函数y=f(x-1)与y=$\frac{1}{2}(x-1)$交点的横坐标,
结合函数f(x)为实数集上的奇函数,作出图象如图: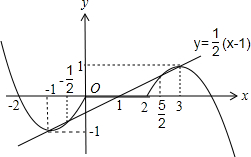
由图可知,函数$y=f(x-1)-\frac{1}{2}(x-1)$的零点个数5个.
故选:D.
点评 本题考查函数零点判定定理,考查了数学转化思想方法和数形结合的解题思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,BC∥AD,PA⊥AD,平面PAB⊥平面ABCD,∠BAD=120°,且$PA=AB=BC=\frac{1}{2}AD=2$.
在四棱锥P-ABCD中,BC∥AD,PA⊥AD,平面PAB⊥平面ABCD,∠BAD=120°,且$PA=AB=BC=\frac{1}{2}AD=2$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂有一排风管,如图所示(单位:厘米),管身为中空的正五棱柱,底面边长为10厘米,高为30厘米,求制作排风管所需的平板下料面积(不考虑排风管的壁厚).
某工厂有一排风管,如图所示(单位:厘米),管身为中空的正五棱柱,底面边长为10厘米,高为30厘米,求制作排风管所需的平板下料面积(不考虑排风管的壁厚).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
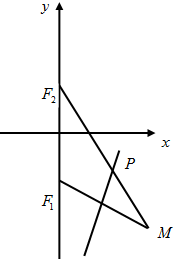 点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.
点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com