
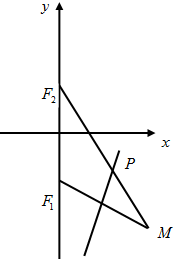
 点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.
点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.分析 (1)连接PF1,推导出|PF1|+|PF2|=4>|F1F2|=2$\sqrt{2}$,由此利用椭圆的定义能求出动点P的轨迹G的方程.
(2)设直线l的方程为y=$\sqrt{2}x+m$,代入椭圆方程,得4x2+2$\sqrt{2}mx$+m2-4=0,由此利用根的判别式、韦达定理、点到直线的距离公式,结合已知条件能求出△QAB面积的最大值.
解答 解:(1)如图,连接PF1,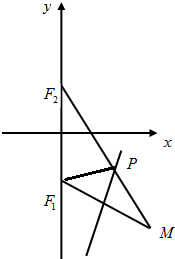
∵|MF2|=4,∴|PM|+|PF2|=4,
又∵|PM|=|PF1|,∴|PF1|+|PF2|=4>|F1F2|=2$\sqrt{2}$,
由椭圆的定义可知动点P的轨迹G是以F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$)为焦点、以2为长轴的椭圆,
∴设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),
则$a=2,c=\sqrt{2}$,∴b=$\sqrt{4-2}=\sqrt{2}$,
∴动点P的轨迹G的方程为$\frac{{y}^{2}}{4}+\frac{{x}^{2}}{2}=1$.
(2)设直线l的方程为y=$\sqrt{2}x+m$,代入椭圆方程,得($\sqrt{2}x+m$)2+2x2=4,
即4x2+2$\sqrt{2}mx$+m2-4=0,
由△=8m2-16(m2-4)=8(8-m2)>0,得m2<8.
又点Q不在直线l上,则m≠0.0<m2<8.
设点A(x1,y1),B(x2,y2),则x1+x2=-$\frac{\sqrt{2}m}{2}$,${x}_{1}{x}_{2}=\frac{{m}^{2}-4}{4}$.
∴|AB|=$\sqrt{1+2}$|x1-x2=$\sqrt{3}$•${\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}}_{\;}$=$\sqrt{3}$•$\sqrt{\frac{{m}^{2}}{2}-({m}^{2}-4)}$=$\sqrt{3}•\sqrt{4-\frac{{m}^{2}}{2}}$.
可得,点Q到直线l的距离d=$\frac{|m|}{\sqrt{3}}$,
则S△QAB=$\frac{1}{2}$|AB|d=$\frac{1}{2}\sqrt{3}•\sqrt{4-\frac{{m}^{2}}{2}}$×$\frac{|m|}{\sqrt{3}}$=$\frac{\sqrt{2}}{4}\sqrt{{m}^{2}(8-{m}^{2})}$.
∵$\sqrt{{m}^{2}(8-{m}^{2})}$≤$\frac{{m}^{2}+8-{m}^{2}}{2}$=4,则S$≤\sqrt{2}$,当且仅当m2=4,即m=±2时取等号.
故△QAB面积的最大值为$\sqrt{2}$.
点评 本题考查椭圆方程的求法,考查三角形面积的最大值的求法,是中档题,解题时要认真审题,注意椭圆的定义、根的判别式、韦达定理、点到直线的距离公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
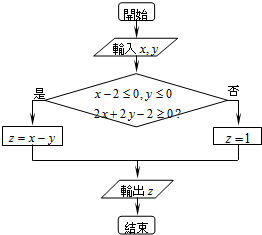 执行如图所示的程序框图,输入的x,y∈R,输出的z的范围为不等式ax2+bx-2≥0(a<0)的解集,则a+b的值为( )
执行如图所示的程序框图,输入的x,y∈R,输出的z的范围为不等式ax2+bx-2≥0(a<0)的解集,则a+b的值为( )| A. | -1 | B. | 1 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7+\sqrt{17}}{4}$ | B. | $\frac{7-\sqrt{17}}{4}$ | C. | $\frac{7+\sqrt{17}}{4}$或$\frac{7-\sqrt{17}}{4}$ | D. | $\frac{7-2\sqrt{17}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com