
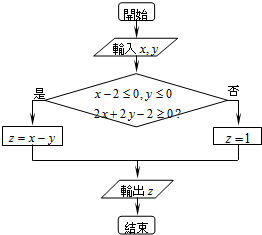
 执行如图所示的程序框图,输入的x,y∈R,输出的z的范围为不等式ax2+bx-2≥0(a<0)的解集,则a+b的值为( )
执行如图所示的程序框图,输入的x,y∈R,输出的z的范围为不等式ax2+bx-2≥0(a<0)的解集,则a+b的值为( )| A. | -1 | B. | 1 | C. | 0 | D. | 2 |
分析 由题意可知$\left\{\begin{array}{l}{x-2≤0}\\{y≤0}\\{2x+2y-2≥0}\end{array}\right.$,其可行域如图所示,求出目标函数z=x-y的范围,即可得到ax2+bx-2≥0(a<0)的解集为(1,3),即可求出a,b的值,问题得以解决.
解答 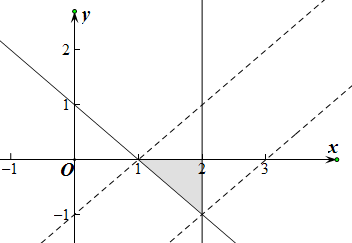 解:由题意可知$\left\{\begin{array}{l}{x-2≤0}\\{y≤0}\\{2x+2y-2≥0}\end{array}\right.$,其可行域如图所示,
解:由题意可知$\left\{\begin{array}{l}{x-2≤0}\\{y≤0}\\{2x+2y-2≥0}\end{array}\right.$,其可行域如图所示,
当z=x-y通过点(1,0)时有最小值,为z=1,
当z=x-y通过点(2,-1)时有最大值,z=2-(-1)=3,
则z的范围为(1,3),
则不等式ax2+bx-2≥0(a<0)的解集(1,3),
则1+3=-$\frac{b}{a}$,1×3=-$\frac{2}{a}$,
解得a=-$\frac{2}{3}$,b=$\frac{8}{3}$,
则a+b=$\frac{8}{3}$-$\frac{2}{3}$=2,
故选:D.
点评 本题截距程序框图考查了线性规划的问题,以及不等式的解集问题,属于中档题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
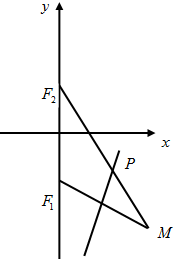 点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.
点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
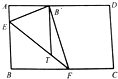 如图,有一张长为16,宽为8的矩形纸片ABCD,以EF为折痕(E在边AB上,F在边BC或CD上),使每次折叠后点B都落在AD边上,此时将B记为B′,过B′作B′T∥CD交EF于T点,则T点的轨迹所在的曲线是( )
如图,有一张长为16,宽为8的矩形纸片ABCD,以EF为折痕(E在边AB上,F在边BC或CD上),使每次折叠后点B都落在AD边上,此时将B记为B′,过B′作B′T∥CD交EF于T点,则T点的轨迹所在的曲线是( )| A. | 双曲线的一支 | B. | 椭圆 | C. | 抛物线 | D. | 直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com