
���� ��1���������ۣ�����Բ�ĵ�ֱ�ߵľ�����ڰ뾶���������̣�������ֱ��l1�ķ��̣�
��2����ֱ��l�ķ���Ϊy=k��x-4����������ԲC2��Բ�ĵ�l�ľ��롢�뾶���ҳ���һ�빹�ɵ�ֱ����������⼴�ɣ�
��3�������P���ֱ��l4��l5�ĵ�бʽ���̣����ݡ�C1�͡�C2�İ뾶����ֱ��l4��ԲC1�صõ��ҳ���ֱ��l5��ԲC2�صõ��ҳ���ȣ��ɵá�C1��Բ�ĵ�ֱ��l4�ľ�����ԲC2��Բ�ĵ�ֱ��l5�ľ�����ȣ������ǿ��Եõ�һ������ֱ��б��k�ķ��̣����������������������ĵ�P�����꣮
��� ��1���⣺�����⣬ֱ�ߵ�б�ʴ���ʱ���跽��Ϊy=k��x-2������kx-y-2k=0��
Բ�ĵ�ֱ�ߵľ���Ϊ$\frac{|2k-5|}{\sqrt{{k}^{2}+1}}$=2����k=$\frac{21}{20}$����ֱ��l1�ķ���y=$\frac{21}{20}$��x-2����
ֱ�ߵ�б�ʲ�����ʱ������Ϊx=2Ҳ�������⣬
����������ֱ��l1�ķ���Ϊy=$\frac{21}{20}$��x-2����x=2��
��2���⣺��ֱ��l2�ķ���Ϊy=k��x-4������ԲC2�صõ��ҳ�Ϊ2$\sqrt{3}$��
��ԲC2��Բ�ĵ�l�ľ���Ϊ1��
�ɵ㵽ֱ��l�ľ��빫ʽ��d=$\frac{|-7k-1|}{\sqrt{{k}^{2}+1}}$=1�����k=0��-$\frac{7}{24}$��
����ֱ��l�ķ���Ϊy=0��y=-$\frac{7}{24}$��x-4����
��3��֤�������P��a��b��������������ɵ�ֱ��l1��l2��б�ʾ������Ҳ�Ϊ0��
������ֱ��l4�ķ���Ϊy-b=k��x-a����k��0
��ֱ��l5����Ϊ��y-b=-$\frac{1}{k}$��x-a����
�ߡ�C1��Բ������Ϊ��4��5�����뾶r1=2��
��C2��Բ������Ϊ��-3��1�����뾶Ϊr2=2��Բ�ľ�O102=3��
��ֱ��l4��ԲC1�صõ��ҳ���ֱ��l5��ԲC2�صõ��ҳ���ȣ�
���C1��Բ�ĵ�ֱ��l4�ľ�����ԲC2��Բ�ĵ�ֱ��l5�ľ�����ȣ�
��$\frac{|��4-a��k+b-5|}{\sqrt{{k}^{2}+1}}$=$\frac{|��1-b��k-3-a|}{\sqrt{1+{k}^{2}}}$
������k��3-a+b��+b+a-2=0��5-b-a��k-a+b-8=0��
��k��ȡֵ����������
��$\left\{\begin{array}{l}{3-a+b=0}\\{a+b-2=0}\end{array}\right.$��$\left\{\begin{array}{l}{5-b-a=0}\\{b-a-8=0}\end{array}\right.$
��$\left\{\begin{array}{l}{a=\frac{5}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{a=-\frac{3}{2}}\\{b=\frac{13}{2}}\end{array}\right.$
��ֱ��l3�ķ�����x=$\frac{5}{2}$��ֱ��l3�ϴ��ڵ�P�������P�������Ի��ഹֱ��l4��l5��
���Ƿֱ���ԲC1��ԲC2�ཻ����ֱ��l4��ԲC1�صõ��ҳ���ֱ��l5��ԲC2�صõ��ҳ���ȣ�
���� ���⿼��㵽ֱ�ߵľ��빫ʽ��ֱ����Բ��λ�ù�ϵ���ԳƵ�֪ʶ��ע�ⷽ�������������������ת��˼�룬�����뷽�̵�˼�룬�������ͣ����е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
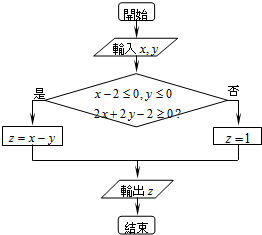 ִ����ͼ��ʾ�ij����ͼ�������x��y��R�������z�ķ�ΧΪ����ʽax2+bx-2��0��a��0���Ľ⼯����a+b��ֵΪ��������
ִ����ͼ��ʾ�ij����ͼ�������x��y��R�������z�ķ�ΧΪ����ʽax2+bx-2��0��a��0���Ľ⼯����a+b��ֵΪ��������| A�� | -1 | B�� | 1 | C�� | 0 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
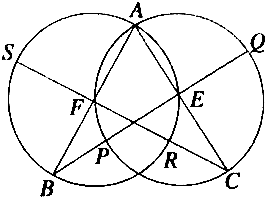 ��ͼ����Բ�ཻ����һ����A����Բ��ֱ��AC��AB������Բ��E��F����B��E��C��F��ֱ�߽���Բ��P��Q��R��S����֤��P��S��Q��R�ĵ㹲Բ��
��ͼ����Բ�ཻ����һ����A����Բ��ֱ��AC��AB������Բ��E��F����B��E��C��F��ֱ�߽���Բ��P��Q��R��S����֤��P��S��Q��R�ĵ㹲Բ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����ABC���DBC�DZ߳���Ϊ2�ĵȱ������Σ���������ƽ�滥�ഹֱ��EA��ƽ��ABC����EA=$\sqrt{3}$��
��ͼ��ʾ����ABC���DBC�DZ߳���Ϊ2�ĵȱ������Σ���������ƽ�滥�ഹֱ��EA��ƽ��ABC����EA=$\sqrt{3}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com