
分析 设A(3cosα,3sinα)(0°≤α≤90°),表示出面积,利用导数,研究函数的最值.
解答 解:设A(3cosα,3sinα)(0°≤α≤90°),则
矩形ABCD面积S=(4-3cosα)•(4-3sinα),
S′=12sinα+12cosα-9=12$\sqrt{2}$sin(α+45°)-9,
∵0°≤α≤90°,
∴45°≤α+45°≤135°,
∴α+45°=90°,即α=45°,Smax=$\frac{41}{2}$-3$\sqrt{2}$,A($\frac{3\sqrt{2}}{2}$,$\frac{3\sqrt{2}}{2}$);
α+45°=45°或135°,即α=0°或90°,Smin=4,A(3,0)或(0,3).
点评 本题考查圆的方程,考查面积的计算,考查导数知识的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
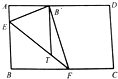 如图,有一张长为16,宽为8的矩形纸片ABCD,以EF为折痕(E在边AB上,F在边BC或CD上),使每次折叠后点B都落在AD边上,此时将B记为B′,过B′作B′T∥CD交EF于T点,则T点的轨迹所在的曲线是( )
如图,有一张长为16,宽为8的矩形纸片ABCD,以EF为折痕(E在边AB上,F在边BC或CD上),使每次折叠后点B都落在AD边上,此时将B记为B′,过B′作B′T∥CD交EF于T点,则T点的轨迹所在的曲线是( )| A. | 双曲线的一支 | B. | 椭圆 | C. | 抛物线 | D. | 直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(α)<g(λ)<g(β)<g(μ) | B. | g(λ)<g(α)<g(β)<g(μ) | C. | g(λ)<g(α)<g(μ)<g(β) | D. | g(α)<g(λ)<g(μ)<g(β) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com