
分析 (Ⅰ)推导出直线$\frac{{x}_{0}x}{3}+\frac{{y}_{0}y}{2}=1$过点P(x0,y0),由$\left\{\begin{array}{l}{\frac{{x}_{0}x}{3}+\frac{{y}_{0}y}{2}=1}\\{\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1}\end{array}\right.$及$2{{x}_{0}}^{2}+3{{y}_{0}}^{2}=6$,得$6{x}^{2}-12{x}_{0}x+3(6-3{{y}_{0}}^{2})=0$,由此能证明直线$\frac{{x}_{0}x}{3}+\frac{{y}_{0}y}{2}=1$是椭圆C在点P处的切线.
(Ⅱ)在$\frac{{x}_{0}x}{3}+\frac{{y}_{0}y}{2}=1$中,令x=1,M(1,$\frac{6-2{x}_{0}}{3{y}_{0}}$),令x=3,得N(3,$\frac{2-2{x}_{0}}{{y}_{0}}$),由此求出|FM|,|FN|,由此能证明$\frac{|FM|}{|FN|}$为定值.
(Ⅲ)求出切线l与x轴的交点为G($\frac{3}{{x}_{0}}$,0),推导出S△ONP=$\frac{3-{x}_{0}}{|{y}_{0}|}$=$\frac{\sqrt{3}}{\sqrt{2}}•\frac{3-{x}_{0}}{\sqrt{3-{{x}_{0}}^{2}}}$,令3-x0=$\frac{1}{t}$,利用配方法能求出△ONP的面积的最小值及对应的P点坐标.
解答 证明:(Ⅰ)∵P(x0,y0)在椭圆C:$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}$=1上,
∴$\frac{{{x}_{0}}^{2}}{3}+\frac{{{y}_{0}}^{2}}{2}=1$,即$\frac{{x}_{0}{x}_{0}}{3}+\frac{{y}_{0}{y}_{0}}{2}=1$,
∴直线$\frac{{x}_{0}x}{3}+\frac{{y}_{0}y}{2}=1$过点P(x0,y0),
由$\left\{\begin{array}{l}{\frac{{x}_{0}x}{3}+\frac{{y}_{0}y}{2}=1}\\{\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,消去y,并利用$2{{x}_{0}}^{2}+3{{y}_{0}}^{2}=6$,得$6{x}^{2}-12{x}_{0}x+3(6-3{{y}_{0}}^{2})=0$,
即6x2-12x0x+6x02=0,即6(x-x0)2=0,∴x=x0,
∴直线$\frac{{x}_{0}x}{3}+\frac{{y}_{0}y}{2}$=1与椭圆C在点P处有且仅有一个交点,
综上,直线$\frac{{x}_{0}x}{3}+\frac{{y}_{0}y}{2}=1$是椭圆C在点P处的切线.
(Ⅱ)在$\frac{{x}_{0}x}{3}+\frac{{y}_{0}y}{2}=1$中,令x=1,得y=$\frac{6-2{x}_{0}}{3{y}_{0}}$,∴M(1,$\frac{6-2{x}_{0}}{3{y}_{0}}$),
在$\frac{{x}_{0}x}{3}+\frac{{y}_{0}y}{2}=1$中,令x=3,得y=$\frac{2-2{x}_{0}}{{y}_{0}}$,∴N(3,$\frac{2-2{x}_{0}}{{y}_{0}}$),
又F(1,0),∴|FM|=|$\frac{6-2{x}_{0}}{3{y}_{0}}$|=2|$\frac{3-{x}_{0}}{3{y}_{0}}$|,
|FN|=$\sqrt{4+(\frac{2-2{x}_{0}}{{y}_{0}})^{2}}$=2$\sqrt{\frac{{{y}_{0}}^{2}+(1-{x}_{0})^{2}}{{{y}_{0}}^{2}}}$=2$\sqrt{\frac{2(1-\frac{{{x}_{0}}^{2}}{3})+(1-2{x}_{0}+{{x}_{0}}^{2})}{{{y}_{0}}^{2}}}$=2$\frac{|{x}_{0}-3|}{\sqrt{3}|{y}_{0}|}$,
∴$\frac{|FM|}{|FN|}$=$\frac{\sqrt{3}}{3}$为定值.
解:(Ⅲ)在直线$\frac{{x}_{0}x}{3}+\frac{{y}_{0}y}{2}=1$中,令y=0,得x=$\frac{3}{{x}_{0}}$,
∴切线l与x轴的交点为G($\frac{3}{{x}_{0}}$,0),
S△ONP=$\frac{3-{x}_{0}}{\sqrt{2(1-\frac{{{x}_{0}}^{2}}{3})}}$=$\frac{\sqrt{3}(3-{x}_{0})}{\sqrt{2}(3-{{x}_{0}}^{2})}$=$\frac{\sqrt{3}}{\sqrt{2}}•\frac{3-{x}_{0}}{\sqrt{3-{{x}_{0}}^{2}}}$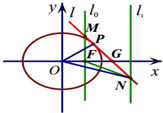
=$\frac{1}{2}$•|$\frac{3}{{x}_{0}}$|•|${y}_{0}-\frac{2-2{x}_{0}}{{y}_{0}}$|
=$\frac{1}{2}$•|$\frac{3}{{x}_{0}}$|•|$\frac{{{y}_{0}}^{2}-2+2{x}_{0}}{{y}_{0}}$|
=$\frac{1}{2}•|\frac{3}{{x}_{0}}|•|\frac{2(1-\frac{{{x}_{0}}^{2}}{3})-2+2{x}_{0}}{{y}_{0}}|$
=|$\frac{3-{x}_{0}}{{y}_{0}}$|=$\frac{3-{x}_{0}}{|{y}_{0}|}$,
S△ONP=$\frac{3-{x}_{0}}{\sqrt{2(1-\frac{{{x}_{0}}^{2}}{3})}}$=$\frac{\sqrt{3}(3-{x}_{0})}{\sqrt{2(1-\frac{{{x}_{0}}^{2}}{3})}}$=$\frac{\sqrt{3}(3-{x}_{0})}{\sqrt{2(3-{{x}_{0}}^{2})}}$=$\frac{\sqrt{3}}{\sqrt{2}}•\frac{3-{x}_{0}}{\sqrt{3-{{x}_{0}}^{2}}}$,
令3-x0=$\frac{1}{t}$,由-$\sqrt{3}<{x}_{0}<\sqrt{3}$,得$\frac{3-\sqrt{3}}{6}<t<\frac{3+\sqrt{3}}{6}$,且t$≠\frac{1}{3}$,
且$\sqrt{3-{{x}_{0}}^{2}}$=$\sqrt{3-(3-\frac{1}{t})^{2}}$=$\sqrt{-\frac{1}{{t}^{2}}+\frac{6}{t}-6}$=$\frac{\sqrt{3}}{\sqrt{2}}$•$\frac{1}{\sqrt{-6{t}^{2}+6t-1}}$=$\frac{\sqrt{3}}{\sqrt{2}}•\frac{1}{\sqrt{-6(t-\frac{1}{2})^{2}+\frac{1}{2}}}$,
∴当t=$\frac{1}{2}$,x0=1时,△ONP(O为坐标原点)的面积是存在最小值{S△ONP}min=$\sqrt{3}$,
此时P(1,$±\frac{2\sqrt{3}}{3}$).
点评 本题考查椭圆的切线方程的证明,考查$\frac{|FM|}{|FN|}$为定值的证明与求法,考查△ONP(O为坐标原点)的面积是否存在最小值的判断与求法,是中档题,解题时要认真审题,注意椭圆性质及配方法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
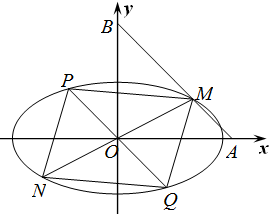 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为4,椭圆的离心率为$\frac{\sqrt{3}}{2}$.设点M是椭圆上不在坐标轴上的任意一点,过点M的直线分别交x轴、y轴于A、B两点上,且满足$\overrightarrow{AM}$=$\frac{1}{3}$$\overrightarrow{AB}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为4,椭圆的离心率为$\frac{\sqrt{3}}{2}$.设点M是椭圆上不在坐标轴上的任意一点,过点M的直线分别交x轴、y轴于A、B两点上,且满足$\overrightarrow{AM}$=$\frac{1}{3}$$\overrightarrow{AB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
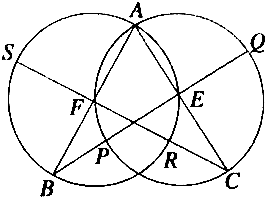 如图,两圆相交,过一交点A引两圆的直径AC、AB,交两圆于E、F,过B、E及C、F的直线交两圆于P、Q、R、S.求证:P、S、Q、R四点共圆.
如图,两圆相交,过一交点A引两圆的直径AC、AB,交两圆于E、F,过B、E及C、F的直线交两圆于P、Q、R、S.求证:P、S、Q、R四点共圆.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com