
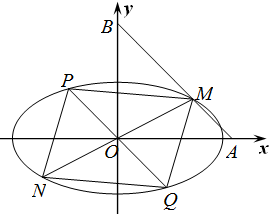
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为4,椭圆的离心率为$\frac{\sqrt{3}}{2}$.设点M是椭圆上不在坐标轴上的任意一点,过点M的直线分别交x轴、y轴于A、B两点上,且满足$\overrightarrow{AM}$=$\frac{1}{3}$$\overrightarrow{AB}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为4,椭圆的离心率为$\frac{\sqrt{3}}{2}$.设点M是椭圆上不在坐标轴上的任意一点,过点M的直线分别交x轴、y轴于A、B两点上,且满足$\overrightarrow{AM}$=$\frac{1}{3}$$\overrightarrow{AB}$.分析 (1)由椭圆长轴长为4,离心率为$\frac{\sqrt{3}}{2}$,求出椭圆方程,由此利用$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$,且A、B分别在x轴、y轴上,能证明AB为定值.
(2)设P(x0,y0),由AB∥PQ,得kPQ=kAB=-$\frac{2{y}_{0}}{{x}_{0}}$,${{x}_{0}}^{2}+4{{y}_{0}}^{2}$=4,直线PQ的方程为:y=-$\frac{2{y}_{0}}{{x}_{0}}x$,由此利用点到直线距离公式、弦长公式能求出结果.
解答 证明:(1)∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为4,椭圆的离心率为$\frac{\sqrt{3}}{2}$.
∴由题意得:$\left\{\begin{array}{l}{2a=4}\\{e=\frac{c}{a}=\frac{\sqrt{3}}{2}}\end{array}\right.$,解得a=2,c=$\sqrt{3}$,
∴b=$\sqrt{4-3}=1$,
∴椭圆方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$,…(3分)
设M(x1,y1),则$\frac{{{x}_{1}}^{2}}{4}+{{y}_{1}}^{2}$=1,
∵$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$,且A、B分别在x轴、y轴上,∴A($\frac{3}{2}{x}_{1}$,0),B(0,3y1),
∴$A{B}^{2}=\frac{9}{4}{{x}_{1}}^{2}+9{{y}_{1}}^{2}=9(\frac{{{x}_{1}}^{2}}{4}+{{y}_{1}}^{2})=9$,
∴AB=3为定值. …(7分)
解:(2)设P(x0,y0),∵AB∥PQ,
∴kPQ=kAB=-$\frac{2{y}_{0}}{{x}_{0}}$,${{x}_{0}}^{2}+4{{y}_{0}}^{2}$=4,
则直线PQ的方程为:y=-$\frac{2{y}_{0}}{{x}_{0}}x$,…(9分)
∵$\left\{\begin{array}{l}{y=-\frac{2{y}_{0}}{{x}_{0}}x}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,∴$\left\{\begin{array}{l}{{{x}_{0}}^{2}=\frac{4{{x}_{0}}^{2}}{{{x}_{0}}^{2}+16{{y}_{0}}^{2}}}\\{{{y}_{0}}^{2}=\frac{16{{y}_{0}}^{2}}{{{x}_{0}}^{2}+16{{y}_{0}}^{2}}}\end{array}\right.$,
∴PQ2=4OP2=4•$\frac{4{{x}_{0}}^{2}+16{{y}_{0}}^{2}}{{{x}_{0}}^{2}16{y}_{0}{\;}^{2}}$=$\frac{64}{{{x}_{0}}^{2}+16{{y}_{0}}^{2}}$,
点M到直线PQ:2y0x+x0y=0的距离:d=$\frac{|2{x}_{0}{y}_{0}+{x}_{0}{y}_{0}|}{\sqrt{4{{y}_{0}}^{2}+{{x}_{0}}^{2}}}$=$\frac{|3{x}_{1}{y}_{1}|}{2}$,…(12分)
∴S四边形MPNQ=2S△MPQ=2×$\frac{1}{2}$×PQ×d=$\frac{8}{\sqrt{{{x}_{0}}^{2}+16{{y}_{0}}^{2}}}$•$\frac{3|{x}_{0}{y}_{0}|}{2}$
=12$\sqrt{\frac{{{x}_{0}}^{2}{{y}_{0}}^{2}}{{{x}_{0}}^{2}+16{{y}_{0}}^{2}}}$=12$\sqrt{\frac{{{x}_{0}}^{2}{{y}_{0}}^{2}}{{{x}_{0}}^{2}+16{{y}_{0}}^{2}}}$=12$\sqrt{\frac{(4-4{y}_{0})^{2}{{y}_{0}}^{2}}{4-4{{y}_{0}}^{2}+16{{y}_{0}}^{2}}}$=12$\sqrt{\frac{-{{y}_{0}}^{4}+{{y}_{0}}^{2}}{3{{y}_{0}}^{2}+1}}$,
令t=3y02+1,t≥1,则$\frac{-{{y}_{0}}^{4}+{y}_{0}}{3{{y}_{0}}^{2}+1}$=$\frac{-(\frac{t-1}{3})^{2}+\frac{t-1}{3}}{t}$=-$\frac{1}{9}(t+\frac{4}{t}-5)≤\frac{1}{9}$,
当且仅当t=2时,取等号,
即3y02+1=2时,(S四边形MPNQ)max=4,
此时${{y}_{0}}^{2}=\frac{1}{3},{{x}_{0}}^{2}=\frac{8}{3}$,
∴${k}_{MN}=±\frac{\sqrt{2}}{4}$.…(16分)
点评 本题考查线段的长是一定值的证明,考查四边形面积的最大值的求出,并求出此时直线的斜率,是中档题,解题时要认真审题,注意椭圆性质的合理运用.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
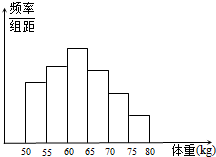 某校对高三年级的学生进行体检,现将高三男生的体重(单位:kg)数据进行整理后分成六组,并绘制频率分布直方图(如图).已知图中从左到右第一、第六小组的频率分别为0.16、0.07,第一、第二、第三小组的频率成等比数列,第三、第四、第五、第六小组的频率成等差数列,且第三小组的频数为236,则该校高三年级的男生总数为( )
某校对高三年级的学生进行体检,现将高三男生的体重(单位:kg)数据进行整理后分成六组,并绘制频率分布直方图(如图).已知图中从左到右第一、第六小组的频率分别为0.16、0.07,第一、第二、第三小组的频率成等比数列,第三、第四、第五、第六小组的频率成等差数列,且第三小组的频数为236,则该校高三年级的男生总数为( )| A. | 800 | B. | 960 | C. | 944 | D. | 888 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com