
���� ��1�������⻭��ͼ�Σ���ͼ�ɵã�|NQ|+|MQ|=|MP|=4��˵������Q�Ĺ켣����N��MΪ���㣬��2Ϊ���������Բ����һ�������켣���̣�
��2����ֱ�ߵ�б�ʴ��ںͲ����ڷ��࣬б�ʲ�����ʱ��ֱ�����A��B������ɵá�AOB����������õ�D�����ꣻ��б�ʴ���ʱ�����ֱ�߷��̣�����Բ�������������ø���ϵ���Ĺ�ϵ����ҳ���ʽ���|AB|�����ֵ����һ����á�AOB����������ֵ�������D�����꣬�ۺϺ�ɵô𰸣�
��� �⣺��1��ԲM����x-$\sqrt{3}$��2+y2=16��N��-$\sqrt{3}$��0����
��ͼ��
��$\overrightarrow{NC}$=$\frac{1}{2}$$\overrightarrow{NP}$����CΪ�߶�NP���е㣬��$\overrightarrow{CQ}$•$\overrightarrow{NP}$=0��
��CQ��NP����|NQ|=|PQ|����|NQ|+|MQ|=|MP|=4��
��|MN|=$2\sqrt{3}��4$��
�ද��Q�Ĺ켣����N��MΪ���㣬��2Ϊ���������Բ��
��b2=a2-c2=1����E�ķ���Ϊ$\frac{{x}^{2}}{4}+{y}^{2}=1$��
��2����ͼ��
������б�ʲ�����ʱ����${y}^{2}=1-\frac{1}{4}=\frac{3}{4}$����y=$��\frac{\sqrt{3}}{2}$��
��|AB|=$\sqrt{3}$����AOB�����S=$\frac{1}{2}��1��\sqrt{3}=\frac{\sqrt{3}}{2}$��
��ʱD��-1��0����1��0����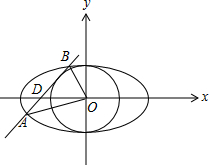
�����ߵ�б�ʴ���ʱ�������߷���Ϊy=kx+m��k��0����
��$\frac{|m|}{\sqrt{{k}^{2}+1}}=1$����m2=1+k2��
����$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$���ã�1+4k2��x2+8kmx+4m2-4=0��
��=64k2m2-4��1+4k2����4m2-4��=48k2��0��
��A��x1��y1����B��x2��y2����
��${x}_{1}+{x}_{2}=\frac{-8km}{1+4{k}^{2}}��{x}_{1}{x}_{2}=\frac{4{m}^{2}-4}{1+4{k}^{2}}$��
��|AB|=$\sqrt{1+{k}^{2}}\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}\sqrt{��\frac{-8km}{1+4{k}^{2}}��^{2}-4\frac{4{m}^{2}-4}{1+4{k}^{2}}}$
=$\sqrt{1+{k}^{2}}•\sqrt{\frac{48{k}^{2}}{��1+4{k}^{2}��^{2}}}$=$\sqrt{\frac{48{k}^{4}+48{k}^{2}}{��1+4{k}^{2}��^{2}}}$=$\sqrt{3}•\sqrt{\frac{��4{k}^{2}+1��^{2}+2��4{k}^{2}+1��-3}{��4{k}^{2}+1��^{2}}}$
=$\sqrt{3}•\sqrt{-\frac{3}{��4{k}^{2}+1��^{2}}+2\frac{1}{4{k}^{2}+1}+1}$��
�൱$\frac{1}{4{k}^{2}+1}=\frac{1}{3}$ʱ��|AB|�����ֵΪ2�����AOB����������ֵΪ$\frac{1}{2}��2��1=1$��
��ʱk=$��\frac{\sqrt{2}}{2}$��m=$��\frac{\sqrt{6}}{2}$��ֱ�߷������������ֱ�Ϊ$y=��\frac{\sqrt{2}}{2}x+\frac{\sqrt{6}}{2}$��y=$��\frac{\sqrt{2}}{2}-\frac{\sqrt{6}}{2}$��
D��������$��\sqrt{3}��0$����
���ϣ���AOB����������ֵΪ1��D������Ϊ��$��\sqrt{3}��0$����
���� ���⿼����Բ�ļ����ʣ�����ֱ����Բ���߹�ϵ��Ӧ�ã�������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������S-ABC����߳�Ϊ2$\sqrt{3}$��������SA���������O������SAD���ڡ�SAD�У���SA=AD���������������ɶ���ǵ�����ֵ��
��֪������S-ABC����߳�Ϊ2$\sqrt{3}$��������SA���������O������SAD���ڡ�SAD�У���SA=AD���������������ɶ���ǵ�����ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6�� | B�� | 7�� | C�� | 8�� | D�� | 9�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com