
分析 (1)化椭圆方程为标准式,求出半长轴和短半轴,结合隐含条件求出半焦距,则椭圆的离心率可求;
(2)设出点A,B的坐标分别为(x0,y0),(t,2),其中x0≠0,由OA⊥OB得到$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,用坐标表示后,把t用含有A点的坐标表示,然后分A,B的横坐标相等和不相等,写出直线AB的方程,然后由圆x2+y2=2的圆心到AB的距离和圆的半径相等,说明直线AB与圆x2+y2=2相切.
解答 解:(1)椭圆C:x2+2y2=4,即为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1,
可得a=2,b=$\sqrt{2}$,c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{2}$,
离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$;
(2)直线AB与圆x2+y2=2相切.
证明如下:
设点A,B的坐标分别为(x0,y0),(t,2),其中x0≠0.
∵OA⊥OB,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,即tx0+2y0=0,
解得t=-$\frac{2{y}_{0}}{{x}_{0}}$,
当x0=t时,y0=-$\frac{1}{2}$t2,代入椭圆C的方程,得t=±$\sqrt{2}$.
故直线AB的方程为x=±$\sqrt{2}$,
圆心O到直线AB的距离d=$\sqrt{2}$.
此时直线AB与圆x2+y2=2相切.
当x0≠t时,直线AB的方程为y-2=$\frac{{y}_{0}-2}{{x}_{0}-t}$(x-t),
即(y0-2)x-(x0-t)y+2x0-ty0=0.
圆心O到直线AB的距离d=$\frac{|2{x}_{0}-t{y}_{0}|}{\sqrt{({y}_{0}-2)^{2}+({x}_{0}-t)^{2}}}$.
又x02+2y02=4,t=-$\frac{2{y}_{0}}{{x}_{0}}$,
故d=$\frac{|2{x}_{0}+\frac{2{{y}_{0}}^{2}}{{x}_{0}}|}{\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}+\frac{4{{y}_{0}}^{2}}{{{x}_{0}}^{2}}+4}}$=$\frac{|\frac{4+{{x}_{0}}^{2}}{{x}_{0}}|}{\sqrt{\frac{{{x}_{0}}^{4}+8{{x}_{0}}^{2}+16}{2{{x}_{0}}^{2}}}}$=$\sqrt{2}$.
此时直线AB与圆x2+y2=2相切.
点评 本题考查椭圆的简单几何性质,考查了圆与圆锥曲线的综合,训练了由圆心到直线的距离判断直线和圆的位置关系,体现了分类讨论的数学思想方法,考查了计算能力和逻辑思维能力,属于难题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,△ABC与△DBC是边长均为2的等边三角形,且所在两平面互相垂直,EA⊥平面ABC,且EA=$\sqrt{3}$.
如图所示,△ABC与△DBC是边长均为2的等边三角形,且所在两平面互相垂直,EA⊥平面ABC,且EA=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
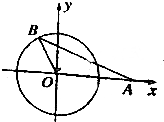 如图所示,圆O的圆心为坐标原点,B为圆O上一点,若点A坐标为(3,0),|AB|=4,sin∠AOB=$\frac{\sqrt{15}}{4}$.
如图所示,圆O的圆心为坐标原点,B为圆O上一点,若点A坐标为(3,0),|AB|=4,sin∠AOB=$\frac{\sqrt{15}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com