
分析 如图所示,取BD的中点O,连接AO,CO.不妨设AD=2.
①取BD的中点,连接OA,OC.利用等腰三角形的性质可得:AO⊥BD,CO⊥BD,再利用线面垂直的判定与性质定理即可判断出结论;
②由已知可得OA=OC═OB=OD=$\sqrt{2}$,AO⊥平面BCD,利用勾股定理可得AC=2,即可判断出正误.
③由②可得:AO⊥平面BCD,因此∠ABO=45°是AB与平面BCD所成的角,即可判断出正误;
④分别取AD,BC的中点E,F,连接OE,OF,EF.可得OE∥AB,OF∥CD,∠EOF或其补角是异面直线AB与CD所成的角,OE=OF=1,利用余弦定理、勾股定理即可得出.
解答 解:如图所示,取BD的中点O,连接AO,CO. 不妨设AD=2.
不妨设AD=2.
①取BD的中点,连接OA,OC.∵AB=AD=CB=CD,∴AO⊥BD,CO⊥BD,又OA∩OC=O,∴BD⊥平面OAC,AC?平面OAC,∴AC⊥BD,正确;
②∵AB=AD=CB=CD,∠BAD=∠BCD=90°,∴OA=OC═OB=OD=$\sqrt{2}$,由①可得:AO⊥平面BCD,∴AO⊥OC,∴AC=2,
∴△ACD是等边三角形,正确;
③由②可得:AO⊥平面BCD,∴∠ABO=45°,是AB与平面BCD所成的角,因此不正确;
④分别取AD,BC的中点E,F,连接OE,OF,EF.则OE∥AB,OF∥CD,∴∠EOF或其补角是异面直线AB与CD所成的角,OE=OF=1.
在平面ABD内过点E作EM⊥BD,垂足为M,连接FM,则EM⊥平面BCD,∴EM⊥FM,FM2=${1}^{2}+(\frac{1}{2})^{2}-2×1×\frac{1}{2}$×cos135°=$\frac{5+2\sqrt{2}}{4}$.
EF2=EM2+FM2=$(\frac{\sqrt{2}}{2})^{2}$+$\frac{5+2\sqrt{2}}{4}$=$\frac{7+2\sqrt{2}}{4}$.∴cos∠EOF=$\frac{1+1-\frac{5+2\sqrt{2}}{4}}{2×1×1}$=$\frac{3-2\sqrt{2}}{8}$,因此∠EOF不是60°或120°,因此不正确.
综上可得:正确的是①②.
故答案为:①②.
点评 本题考查了线面面面垂直的判定与性质定理、等边三角形与等腰三角形的性质、异面直线所成的角、余弦定理勾股定理,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
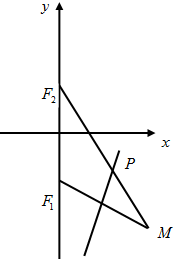 点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.
点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知空间四边形ABCD的各边和对角线的长都等于a,点M、N分别是AB、CD的中点.
如图所示,已知空间四边形ABCD的各边和对角线的长都等于a,点M、N分别是AB、CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com