
���� ����������f��x���ڵ㣨1��f��1������������Ϊy=0���ɵ�f'��1��=0��������ʵ��a��ֵ��
����������f��x���ڶ������ϲ��������������ۣ���϶��κ�����������a��ȡֵ��Χ��
������$k��\frac{2e}{{{e^2}-1}}a-2$����$\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}��\frac{2e}{{{e^2}-1}}$���ɣ���֪��������x1�ʣ�0��1����x2�ʣ�1��+�ޣ�����x1•x2=1�����x1-x2��$\frac{{e}^{2}-1}{2e}$��lnx1-lnx2������$\frac{1}{{x}_{2}}$-x2+$\frac{{e}^{2}-1}{2e}$lnx2��0��x2�ʣ�1��+�ޣ������캯�����������a��ȡֵ���ϣ�
��� �⣺����f��x���Ķ�����Ϊ��0��+�ޣ�������$f'��x��=-\frac{1}{x^2}-1+\frac{a}{x}=-\frac{{{x^2}-ax+1}}{x^2}$��
��f'��1��=0����a=2��
����f��x���Ķ�����Ϊ��0��+�ޣ�������$f'��x��=-\frac{1}{x^2}-1+\frac{a}{x}=-\frac{{{x^2}-ax+1}}{x^2}$��
��g��x��=x2-ax+1�����б�ʽ��=a2-4������֪���С���0����a��-2��a��2��
�ٵ�a��-2ʱ��g��x���ĶԳ���$x=\frac{a}{2}��1$��g��0��=1��0����x�ʣ�0��+�ޣ�ʱ��g��x����0��
��f�䣨x����0����f��x���ڣ�0��+�ޣ��ϵ����ݼ����������⣻
�ڵ�a��2ʱ��g��x���ĶԳ���$x=\frac{a}{2}��1$��g��0��=1��0����g��x��=0����������x1��x2����x1�ʣ�0��1����x2�ʣ�1��+�ޣ���x1•x2=1��
��x�ʣ�0��x1����x�ʣ�x2��+�ޣ�ʱ��f�䣨x����0����x�ʣ�x1��x2��ʱ��f�䣨x����0��
��f��x���ڣ�0��x1������x2��+�ޣ��ϵ����ݼ����ڣ�x1��x2���ϵ���������
���Ͽ�֪��a��ȡֵ��ΧΪ��2��+�ޣ���
�������������������a���ɣ�1��֪a��2��
��Ϊ$f��{x_1}��-f��{x_2}��=\frac{{{x_2}-{x_1}}}{{{x_1}{x_2}}}+��{x_2}-{x_1}��+a��ln{x_1}-ln{x_2}��$��
����$k=\frac{{f��{x_1}��-f��{x_2}��}}{{{x_1}-{x_2}}}=-\frac{1}{{{x_1}{x_2}}}-1+a\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}$��
��$k��\frac{2e}{{{e^2}-1}}a-2$����$\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}��\frac{2e}{{{e^2}-1}}$��
�ɣ�1��֪��������x1�ʣ�0��1����x2�ʣ�1��+�ޣ�����x1•x2=1��
���x1-x2��$\frac{{e}^{2}-1}{2e}$��lnx1-lnx2������$\frac{1}{{x}_{2}}$-x2+$\frac{{e}^{2}-1}{2e}$lnx2��0��x2�ʣ�1��+�ޣ� ����*��
��F��x��=$\frac{1}{x}$-x+$\frac{{e}^{2}-1}{e}$lnx��x��1����
����x1��=$\frac{1}{2}$[$\frac{{e}^{2}-1}{2e}$-$\sqrt{��\frac{{e}^{2}-1}{2e}��^{2}-4}$]��x2��=$\frac{1}{2}$[$\frac{{e}^{2}-1}{2e}$+$\sqrt{��\frac{{e}^{2}-1}{2e}��^{2}-4}$]��
���ɣ�1����֪��F��x����$��1��x_2^/��$�ϵ�����������$��x_2^/��+�ޣ�$�ϵ����ݼ�����$0��x_1^/��1��x_2^/��e$��
��F��1��=F��e��=0�����Ե�x�ʣ�1��e��ʱ��F��x����0����x�ʣ�e��+�ޣ�ʱ��F��x����0��
�ɷ��̣�*��֪��F��x2����0������x2��e��
���ɣ�1��֪$g��{x_2}��=x_2^2-a{x_2}+1=0$��֪$a={x_2}+\frac{1}{x_2}��e+\frac{1}{e}$����$y=x+\frac{1}{x}$��[e+�ޣ��ϵ�����������
��a��2�����a��ȡֵ������$\{a|a��e+\frac{1}{e}\}$��
���� ���⿼�鵼��֪ʶ���ۺ����ã����鵼���ļ������壬���麯���ĵ����ԣ�����������۵���ѧ˼�룬����ѧ���������������������������⣮


 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7+\sqrt{17}}{4}$ | B�� | $\frac{7-\sqrt{17}}{4}$ | C�� | $\frac{7+\sqrt{17}}{4}$��$\frac{7-\sqrt{17}}{4}$ | D�� | $\frac{7-2\sqrt{17}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
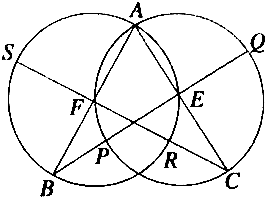 ��ͼ����Բ�ཻ����һ����A����Բ��ֱ��AC��AB������Բ��E��F����B��E��C��F��ֱ�߽���Բ��P��Q��R��S����֤��P��S��Q��R�ĵ㹲Բ��
��ͼ����Բ�ཻ����һ����A����Բ��ֱ��AC��AB������Բ��E��F����B��E��C��F��ֱ�߽���Բ��P��Q��R��S����֤��P��S��Q��R�ĵ㹲Բ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
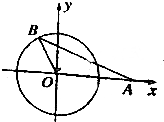 ��ͼ��ʾ��ԲO��Բ��Ϊ����ԭ�㣬BΪԲO��һ�㣬����A����Ϊ��3��0����|AB|=4��sin��AOB=$\frac{\sqrt{15}}{4}$��
��ͼ��ʾ��ԲO��Բ��Ϊ����ԭ�㣬BΪԲO��һ�㣬����A����Ϊ��3��0����|AB|=4��sin��AOB=$\frac{\sqrt{15}}{4}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com