

分析 (1)以AB所在直线为x轴,AB的中垂线为y轴,建立平面直角坐标系xoy,推导出半圆的半径为1米,求出半圆的方程、OD、DM,由此能求出水面的宽度.
(2)为使挖掉的土最少,等腰梯形的两腰必须与半圆相切,由此利用切线方程、导数性质能求出当渠底宽为$\frac{2\sqrt{3}}{3}$米时,所挖的土最少.
解答 解:(1)以AB所在直线为x轴,AB的中垂线为y轴,建立如图所示的平面直角坐标系xoy,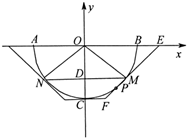
∵AB=2米,∴半圆的半径为1米,
则半圆的方程为x2+y2=1,(-1≤x≤1,y≤0),
∵水深CD=0.4米,∴OD=0.6米,
在Rt△ODM,DM=$\sqrt{O{M}^{2}-O{D}^{2}}$=$\sqrt{1-0.{6}^{2}}$=0.8(米),
∴MN=2DM=1.6米,
∴水面的宽度为1.6米.
(2)为使挖掉的土最少,等腰梯形的两腰必须与半圆相切,
设切点为P(cosθ,sinθ),(-$\frac{π}{2}$<θ<0)为圆弧BC上的一点,
过P作半圆的切线得如图所示的直角梯形OCFE,得切线EF的方程为xcosθ+ysinθ=1,
令y=0,得E($\frac{1}{cosθ}$,0),令y=-1,得F($\frac{1+sinθ}{cosθ}$,-1),
设直线梯形OCFE的面积为S,
则S=(CF+OE)•OC=($\frac{1}{cosθ}$+$\frac{1+sinθ}{cosθ}$)×1=$\frac{2+sinθ}{cosθ}$,(-$\frac{π}{2}$<θ<0),
S′=$\frac{cosθcosθ-(2+sinθ)(-sinθ)}{co{s}^{2}θ}$=$\frac{1+2sinθ}{co{s}^{2}θ}$,
令S′=0,解得θ=-$\frac{π}{6}$,
当-$\frac{π}{2}<θ<-\frac{π}{6}$时,S′<0,函数单调递减;当-$\frac{π}{6}$<θ<0时,S′>0,函数单调递增.
∴$θ=-\frac{π}{6}$时,面积S取得最小值,最小值为$\sqrt{3}$,
此时CF=$\frac{1+sin(-\frac{π}{6})}{cos(-\frac{π}{6})}$=$\frac{\sqrt{3}}{3}$,
即当渠底宽为$\frac{2\sqrt{3}}{3}$米时,所挖的土最少.
点评 本题考查水面的宽度的求法,考查当改挖后的水渠底宽为多少时,所挖出的土量最少的求法,是中档题,解题时要认真审题,注意切线方程、导数性质的合理运用.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{6}$,$\frac{1}{\root{3}{16}}$] | B. | [$\frac{1}{6}$,$\frac{1}{4}$] | C. | [$\frac{1}{9}$,$\frac{1}{\root{3}{16}}$] | D. | [$\frac{1}{9}$,$\frac{1}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com