
| AЃЎ | [$\frac{1}{6}$ЃЌ$\frac{1}{\root{3}{16}}$] | BЃЎ | [$\frac{1}{6}$ЃЌ$\frac{1}{4}$] | CЃЎ | [$\frac{1}{9}$ЃЌ$\frac{1}{\root{3}{16}}$] | DЃЎ | [$\frac{1}{9}$ЃЌ$\frac{1}{4}$] |
ЗжЮі ИљОнЖдШЮвтx1ЃЌx2ЁЪ[-1ЃЌ1]ЃЌЖМга|f3ЃЈx1ЃЉ-f3ЃЈx2ЃЉ|Ём1ЃЌЫЕУїЕБxШЁСНИіЬиЪтжЕ-1КЭ1ЪБ|f3ЃЈ1ЃЉ-f3ЃЈ-1ЃЉ|Ём1ГЩСЂЃЌгЩДЫЧѓГіaЕФГѕВНЗЖЮЇЃЌШЛКѓАбдКЏЪ§f3ЃЈxЃЉЧѓЕМЃЌЕУЕНЕМКЏЪ§ЕФСНИіСуЕуЮЊ-$\sqrt{a}$ЃЌ$\sqrt{a}$ЃЌдйЧѓГіКЏЪ§f3ЃЈxЃЉдкЃЈ-1ЃЌ1ЃЉЩЯЕФМЋДѓжЕКЭМЋаЁжЕЃЌдйгЩМЋДѓжЕКЭМЋаЁжЕВюЕФОјЖджЕаЁгкЕШгк1ЧѓГіaЕФШЁжЕЗЖЮЇЃЌКЭгЩ|f3ЃЈ1ЃЉ-f3ЃЈ-1ЃЉ|Ём1ЧѓГіЕФaЕФЗЖЮЇШЁНЛМЏМДПЩ
НтД№ НтЃКвђЮЊЖдШЮвтx1ЃЌx2ЁЪ[-1ЃЌ1]ЃЌЖМга|f3ЃЈx1ЃЉ-f3ЃЈx2ЃЉ|Ём1ЃЌ
Ыљвд|f3ЃЈ1ЃЉ-f3ЃЈ-1ЃЉ|Ём1ЃЌДгЖјга|ЃЈ-1+3aЃЉ-ЃЈ1-3aЃЉ|=|6a-2|Ём1ЃЌ
Ыљвд$\frac{1}{6}$ЁмaЁм$\frac{1}{2}$ЃЎ
гжf3ЁфЃЈxЃЉ=-3ЃЈx2-aЃЉЃЌ
дк[-1ЃЌ-$\sqrt{a}$]ЃЌ[$\sqrt{a}$ЃЌ1]ФкfЁф3ЃЈxЃЉЃМ0ЃЌ
Ыљвдf3ЃЈxЃЉдк[-1ЃЌ-$\sqrt{a}$]ЃЌ[$\sqrt{a}$ЃЌ1]ФкЮЊМѕКЏЪ§ЃЌ
f3ЃЈxЃЉдк[-$\sqrt{a}$ЃЌ$\sqrt{a}$]ФкЮЊдіКЏЪ§ЃЌ
жЛаш|f3ЃЈ$\sqrt{a}$ЃЉ-f3ЃЈ$\sqrt{a}$ЃЉ|Ём1
ЛЏМђПЩЕУ4a$\sqrt{a}$Ём1ЃЌНтЕУЃКaЁм$\frac{1}{\root{3}{16}}$ЃЎ
ЫљвдaЕФШЁжЕЗЖЮЇЪЧ$\frac{1}{6}$ЁмaЁм$\frac{1}{\root{3}{16}}$ЃЎ
ЙЪбЁЃКAЃЎ
ЕуЦР БОЬтПМВщСЫРћгУЕМЪ§баОПКЏЪ§ЕФзюжЕЃЌПМВщСЫЪ§бЇзЊЛЏЫМЯыЗНЗЈЃЌЪєгавЛЖЈФбЖШЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
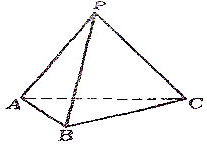 ШчЭМЃЌЕуPЪЧЁїABCдкЦНУцЭтЕФвЛЕуЃЌPA=PB=PC=2ЃЌAB=BC=AC=1ЃЌ
ШчЭМЃЌЕуPЪЧЁїABCдкЦНУцЭтЕФвЛЕуЃЌPA=PB=PC=2ЃЌAB=BC=AC=1ЃЌВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
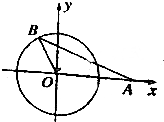 ШчЭМЫљЪОЃЌдВOЕФдВаФЮЊзјБъдЕуЃЌBЮЊдВOЩЯвЛЕуЃЌШєЕуAзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌ|AB|=4ЃЌsinЁЯAOB=$\frac{\sqrt{15}}{4}$ЃЎ
ШчЭМЫљЪОЃЌдВOЕФдВаФЮЊзјБъдЕуЃЌBЮЊдВOЩЯвЛЕуЃЌШєЕуAзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌ|AB|=4ЃЌsinЁЯAOB=$\frac{\sqrt{15}}{4}$ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 дкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊдВC1ЃКЃЈx+3ЃЉ2+y2=4КЭжБЯпlЃК14x+8y-23=0ЃЎ
дкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊдВC1ЃКЃЈx+3ЃЉ2+y2=4КЭжБЯпlЃК14x+8y-23=0ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЃЈ1ЃЌ+ЁоЃЉ | BЃЎ | ЃЈ-ЁоЃЌ$\frac{3}{4}$] | CЃЎ | ЃЈ$\frac{1}{2}$ЃЌ+ЁоЃЉ | DЃЎ | [$\frac{3}{4}$ЃЌ+ЁоЃЉ |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com