
分析 (1)由离心率为$\frac{{\sqrt{3}}}{2}$,椭圆上的点到直线$x=-\frac{{5\sqrt{5}}}{2}$的距离的最大值为$\frac{{9\sqrt{5}}}{2}$,求出a,b,由此能求出椭圆方程.
(2)设直线l的方程为y=x+m,由$\left\{\begin{array}{l}y=x+m\\ \frac{x^2}{20}+\frac{y^2}{5}=1\end{array}\right.$得,5x2+8mx+4m2-20=0,要证直线MA,MB与x轴围成一个等腰三角形,只要证明直线MA,MB的斜率互为相反数,由此能证明直线MA,MB与x轴围成一个等腰三角形.
解答 (本小题满分12分)
解:(1)∵离心率为$\frac{{\sqrt{3}}}{2}$,∴$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,
又椭圆上的点到直线$x=-\frac{{5\sqrt{5}}}{2}$的距离的最大值为$\frac{{9\sqrt{5}}}{2}$,
∴$a+\frac{{5\sqrt{5}}}{2}=\frac{{9\sqrt{5}}}{2}$,则$a=2\sqrt{5}$,∴$c=\sqrt{15}$,…(3分)
b2=a2-c2=20-15=5,
∴椭圆方程为$\frac{x^2}{20}+\frac{y^2}{5}=1$. …(5分)
证明:(2)由题设知,设直线l的方程为y=x+m,
由$\left\{\begin{array}{l}y=x+m\\ \frac{x^2}{20}+\frac{y^2}{5}=1\end{array}\right.$得,5x2+8mx+4m2-20=0,
设A(x1,y1),B(x2,y2),
∴${x_2}+{x_2}=-\frac{8m}{5}$,${x_1}{x_2}=\frac{{4{m^2}-20}}{5}$,…(7分)
要证直线MA,MB与x轴围成一个等腰三角形,
只要证明直线MA,MB的斜率互为相反数即可,…(8分)
设直线MA,MB的斜率分别为k1,k2(k1≠0,k2≠0),
∴${k_1}+{k_2}=\frac{{{y_1}-1}}{{{x_1}-4}}+\frac{{{y_2}-1}}{{{x_2}-4}}$=$\frac{{({y_1}-1)({x_2}-4)+({y_2}-1)({x_1}-4)}}{{({x_1}-4)({x_2}-4)}}$
=$\frac{{({x_1}+m-1)({x_2}-4)+({x_2}+m-1)({x_1}-4)}}{{({x_1}-4)({x_2}-4)}}$
=$\frac{{2{x_1}{x_2}+(m-5)({x_1}+{x_2})-8(m-1)}}{{({x_1}-4)({x_2}-4)}}$
=$\frac{{2×\frac{{4{m^2}-20}}{5}+(m-5)(-\frac{8m}{5})-8(m-1)}}{{({x_1}-4)({x_2}-4)}}$
=$\frac{{8{m^2}-40-8{m^2}+40m-40m+40}}{{5({x_1}-4)({x_2}-4)}}=0$.
故直线MA,MB与x轴围成一个等腰三角形. …(12分)
点评 本题考查椭圆方程的求法,考查直线MA,MB围成一个等腰三角形,是中档题,解题时要认真审题,注意椭圆性质、直线斜率、韦达定理的合理运用.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
 某工厂有一排风管,如图所示(单位:厘米),管身为中空的正五棱柱,底面边长为10厘米,高为30厘米,求制作排风管所需的平板下料面积(不考虑排风管的壁厚).
某工厂有一排风管,如图所示(单位:厘米),管身为中空的正五棱柱,底面边长为10厘米,高为30厘米,求制作排风管所需的平板下料面积(不考虑排风管的壁厚).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{π}{4}$) | B. | (1,$\frac{3π}{4}$) | C. | (1,$\frac{π}{4}$) | D. | (1,$\frac{3π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
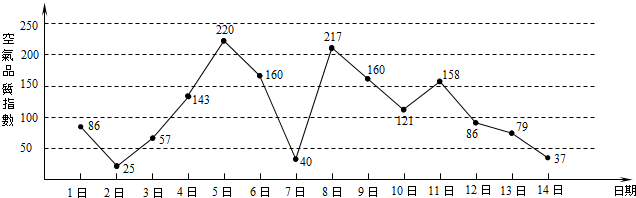
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
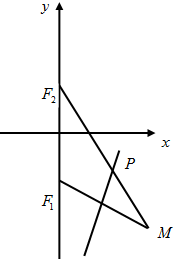 点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.
点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com