
���� ��Ai��ʾ�¼���������3��i�յ�����С���i=1��2��3������13�����������⣬$P��{A_i}��=\frac{1}{13}$����Ai��Aj���⣬i��j=1��2������13��i��j��
��1����BΪ�¼������˵��ﵱ�տ����ض���Ⱦ������B=A5��A8��������Խ����
��2���������֪����պ���һ���������Ϊ�ŵ�ʱ��ΪC���պ��ж����������Ϊ�ŵ�ʱ��ΪD�����ݸ��ʹ�ʽ���㼴�ɣ�
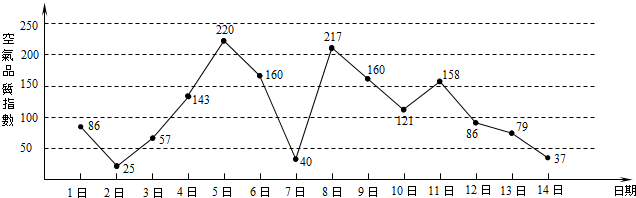
��3����ͼ���֪����3��5�տ�ʼ��������Ŀ�������ָ���������
��� �⣺��Ai��ʾ�¼���������3��i�յ�����С���i=1��2��3������13�����������⣬$P��{A_i}��=\frac{1}{13}$����Ai��Aj���⣬i��j=1��2������13��i��j��
��1����BΪ�¼������˵��ﵱ�տ����ض���Ⱦ������B=A5��A8�����ԣ�$P��B��=P��{{A_5}��{A_8}}��=P��{A_5}��+P��{A_8}��=\frac{2}{13}$
��2���������֪����պ���һ���������Ϊ�ŵ�ʱ��ΪC���պ��ж����������Ϊ�ŵ�ʱ��ΪD��
P��C��=P��A3��A6��A7��A11��=P��A3��+P��A6��+P��A7��+P��A11��=$\frac{4}{13}$��
P��D��=P��A1��A2��A12��A13��=P��A1��+P��A2��+P��A12��+P��A13��=$\frac{4}{13}$��
����ͣ���ڼ��������������1��Ϊ�������¼��ĸ���$P��C��+P��D��=\frac{8}{13}$
��3����3��5�տ�ʼ��������Ŀ�������ָ���������
���� ���⿼���˹ŵ���ͼ�����ʼ��㹫ʽ��ѵ����ѧ���Ķ�ͼ�������ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Բ | B�� | Բ | C�� | ˫���ߵ�һ֧ | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com