
分析 (1)容易看出x增大时f(x)增大,从而得出f(x)在(-∞,0),(0,+∞)上为增函数,从而便可得出f(x)的单调区间;
(2)根据(1)便知函数f(x)在[1,2]上单调递增,从而可求出f(x)在[1,2]上的值域,而根据题意知方程m=f(x)有解,从而便得出m的取值范围.
解答 解:(1)f(x)的定义域为(-∞,0)∪(0,+∞);
x在(-∞,0),或(0,+∞)上增大时,$\frac{1}{x}$减小,$-\frac{1}{x}$增大,$x-\frac{1}{x}$增大;
∴f(x)在(-∞,0),(0,+∞)上为增函数;
即f(x)的单调区间为(-∞,0),(0,+∞);
(2)由(1)知f(x)在[1,2]上单调递增;
∴f(x)在[1,2]上的值域为[f(1),f(2)]=[0,$\frac{3}{2}$];
若函数y=f(x)-m有零点,则m=f(x)有解;
∴m的取值范围为$[0,\frac{3}{2}]$.
点评 考查函数单调性的定义,根据单调性定义判断函数单调性的方法,根据函数单调性定义求函数值域,以及函数零点的定义.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:选择题
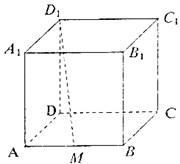 在棱长为2的正方体ABCD-A1B1C1D1中,M为AB的中点,经过点A作D1M的垂面,该垂面被正方体截得部分的面积是( )
在棱长为2的正方体ABCD-A1B1C1D1中,M为AB的中点,经过点A作D1M的垂面,该垂面被正方体截得部分的面积是( )| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{3\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7+\sqrt{17}}{4}$ | B. | $\frac{7-\sqrt{17}}{4}$ | C. | $\frac{7+\sqrt{17}}{4}$或$\frac{7-\sqrt{17}}{4}$ | D. | $\frac{7-2\sqrt{17}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆 | B. | 圆 | C. | 双曲线的一支 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com