
(本题满分12分)设△ABC的内角A,B,C所对边的长分别是a,b,c,且b=4,c=2,A=2B.
(1)求a的值;(2)求sin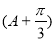 的值.
的值.
(1)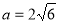 ;(2)
;(2) 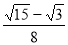 .
.
【解析】
试题分析:(1)利用正弦定理与余弦定理进行求解;(2)先借助(1)步结果,利用余弦定理求出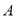 的三角函数值,再利用两角和的正弦公式进行求解
的三角函数值,再利用两角和的正弦公式进行求解 .
.
解题思路: 解三角形,主要涉及三角形的内角和定理、三边大小关系、正弦定理、余弦定理、三角形的面积公式等,往往还与三角恒等变换相联系.
试题解析:(1)因为A=2B,所以sin A=sin 2B=2sin Bcos B, 2分
由余弦定理得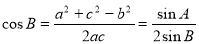 ,
,
所以由正弦定理可得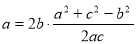 4分
4分
因为b=4,c=2,所以a2=24,即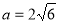 6分
6分
(2) 由余弦定理得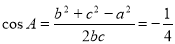 8分
8分
因为0<A<π,所以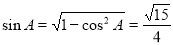
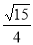 10分
10分
故sin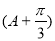 =sin Acos
=sin Acos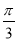 +cos Asin
+cos Asin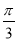 =
=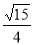 ×
×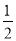 +(
+(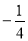 )×
)× =
=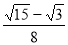 .
.
考点:1.正弦定理;2.余弦定理;二倍角公式;4.两角和的正弦公式.


科目:高中数学 来源:2014-2015学年山东省乐陵市高二上学期期中考试理科数学试卷(解析版) 题型:选择题
对任意a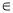 [-1,1],函数
[-1,1],函数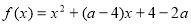 的值恒大于零,则x的取值范围是( )
的值恒大于零,则x的取值范围是( )
A、1<x<3 B、x<1或x>3 C、1<x<2 D、x<1或x>2
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省乐陵市高二上学期期中考试理科数学试卷(解析版) 题型:选择题
设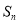 是等差数列
是等差数列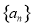 的前n项和,已知
的前n项和,已知 ,
,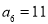 ,则
,则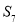 等于( )
等于( )
A、13 B、35 C、49 D、63
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省乐陵市高二上学期期中考试文科数学试卷(解析版) 题型:选择题
在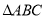 中,角A,B,C的对边分别是a,b,c,若A:B:C=1: 2:3,则a:b:c=( )
中,角A,B,C的对边分别是a,b,c,若A:B:C=1: 2:3,则a:b:c=( )
A、1:2:3 B、2:3:4 C、3:4:5 D、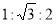
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北邢台一中高二12月月考文科数学试卷(解析版) 题型:选择题
设底面为等边三角形的直棱柱的体积为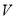 ,那么其表面积最小时,底面边长为( )
,那么其表面积最小时,底面边长为( )
A.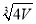 B.
B.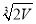 C.
C.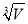 D.
D.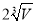
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com