
【题目】已知f(x)=x2-2ax+2(a∈R),当x∈[-1,+∞)时,![]() 恒成立,则a的取值范围是_________.
恒成立,则a的取值范围是_________.
【答案】![]() .
.
【解析】试题分析:g(x)=x2-2ax+2-a,根据对称轴与定义区间位置关系分类讨论:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;解不等式,再求并集得a的取值范围.
;解不等式,再求并集得a的取值范围.
试题解析:解:法一:f(x)=(x-a)2+2-a2,此二次函数图象的对称轴为x=a.
①当a∈(-∞,-1)时,f(x)在[-1,+∞)上单调递增,
f(x)min=f(-1)=2a+3.
要使f(x)≥a恒成立,只需f(x)min≥a,
即2a+3≥a,解得-3≤a<-1;
②当a∈[-1,+∞,)时,f(x)min=f(a)=2-a2,
由2-a2≥a,解得-1≤a≤1.
综上所述,所求a的取值范围为-3≤a≤1.
法二:令g(x)=x2-2ax+2-a,由已知,得
x2-2ax+2-a≥0在[-1,+∞)上恒成立,
即Δ=4a2-4(2-a)≤0或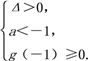
解得-3≤a≤1.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】祖暅原理:“幂势既同,则积不容异”,它是中国古代一个涉及几何体体积问题,意思是两个等高的几何体,如在同高处的截面积恒相等,则体积相等,设A,B为两个等高的几何体,p:A,B的体积相等,q:A,B在同高处的截面积不恒相等,根据祖暅原理可知,q是-p的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形ABCD中,E、F分别是AB、CD上的点,BE=CF=1,BC=2,AB=CD=3,P、Q分别为DE、CF的中点,现沿着EF翻折,使得二面角A﹣EF﹣B大小为 ![]() .
.
(Ⅰ)求证:PQ∥平面BCD;
(Ⅱ)求二面角A﹣DB﹣E的余弦值.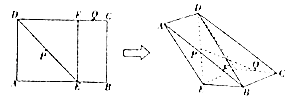
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的面积为3,且满足0≤![]() ≤6,设
≤6,设![]() 与
与![]() 的夹角为θ.
的夹角为θ.
(1)求θ的取值范围;
(2)求函数f(θ)=2sin2![]() -
-![]() (cos θ+sin θ)·(cos θ-sin θ)的最大值与最小值.
(cos θ+sin θ)·(cos θ-sin θ)的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的中心在原点焦点在
的中心在原点焦点在 ![]() 轴上,离心率等于
轴上,离心率等于 ![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 ![]() 的焦点.
的焦点.
(1)求椭圆 ![]() 的焦点;
的焦点;
(2)已知点 ![]() 在椭圆
在椭圆 ![]() 上,点
上,点 ![]() 是椭圆
是椭圆 ![]() 上不同于
上不同于 ![]() 的两个动点,且满足:
的两个动点,且满足: ![]() ,试问:直线
,试问:直线 ![]() 的斜率是否为定值?请说明理由.
的斜率是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是数列
是数列 ![]() 的前
的前 ![]() 项和,并且
项和,并且 ![]() ,对任意正整数
,对任意正整数 ![]() ,
, ![]() ,设
,设 ![]() (
( ![]() ).
).
(1)证明:数列 ![]() 是等比数列,并求
是等比数列,并求 ![]() 的通项公式;
的通项公式;
(2)设 ![]() ,求证:数列
,求证:数列 ![]() 不可能为等比数列.
不可能为等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com