
| A.ei越小越好 | B.
| ||||||||
C.
| D.
|
科目:高中数学 来源:不详 题型:解答题
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 总计 | | | 210 |
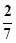 .
.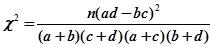 ,其中
,其中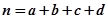 .
.| 参考数据 | 当 ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
当 >2.706时,有90%的把握判定变量A,B有关联; >2.706时,有90%的把握判定变量A,B有关联; | |
当 >3.841时,有95%的把握判定变量A,B有关联; >3.841时,有95%的把握判定变量A,B有关联; | |
当 >6.635时,有99%的把握判定变量A,B有关联. >6.635时,有99%的把握判定变量A,B有关联. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
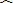 |
| y |
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A.0.5 | B.0.6 | C.0.7 | D.0.8 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 学生的编号 | 1 | 2 | 3 | 4 | 5 |
| 数学成绩xi | 80 | 75 | 70 | 65 | 60 |
| 物理成绩yi | 70 | 66 | 68 | 64 | 62 |
| 5 |
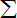 |
| i=1 |
| 5 |
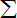 |
| i=1 |
| x | 2i |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 |
| y |
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A.3.25 | B.2.6 | C.2.2 | D.0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 40 | ||
| 学习积极性一般 | 30 | ||
| 合计 | 100 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.100个吸烟者中至少有99个患慢性支气管炎 |
| B.某个人吸烟,那么这个人有99%的概率患有慢性支气管炎 |
| C.在100个吸烟者中一定有患慢性支气管炎的人 |
| D.在100个吸烟者中可能一个患慢性支气管炎的人都没有 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com