
【题目】如图,在三棱柱![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
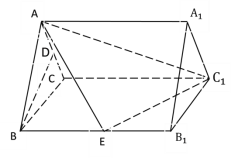
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)若这个三棱柱的底面是等边三角形,侧面都是正方形,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析; (Ⅱ)![]() .
.
【解析】
(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明四边形
,证明四边形![]() 为平行四边形,可得出
为平行四边形,可得出![]() ,再利用直线与平面平行的判定定理可证明出
,再利用直线与平面平行的判定定理可证明出![]() 平面
平面![]() ;
;
(Ⅱ)取![]() 、
、![]() 的中点
的中点![]() 、
、![]() ,连接
,连接![]() 、
、![]() ,证明出
,证明出![]() 平面
平面![]() 以及
以及![]() ,然后以点
,然后以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,计算出平面
,计算出平面![]() 和平面
和平面![]() 的法向量,利用空间向量法求出二面角
的法向量,利用空间向量法求出二面角![]() 的余弦值.
的余弦值.
(Ⅰ)证明:取![]() 的中点为
的中点为![]() ,连接
,连接![]() 、
、![]() .
.
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,且
,且![]() ,
,
![]() 为
为![]() 的中点,
的中点,![]() 且
且![]() .
.
![]() 且
且![]() ,
,![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(Ⅱ)解:设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,
![]() 为等边三角形 ,∴
为等边三角形 ,∴![]()
![]() 侧面都是正方形 ,
侧面都是正方形 ,![]() ,
,![]() ,
,
![]() 、
、![]() 平面
平面![]() 且
且![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
取![]() 中点为
中点为![]() ,连接
,连接![]() ,则
,则![]() .
.
以![]() 为原点,以
为原点,以![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,如图.
,如图.
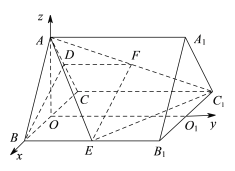
设![]() ,则
,则![]() 、
、![]() 、
、![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则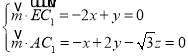 ,
,
令![]() ,得
,得![]() ,
,
取平面![]() 的法向量为
的法向量为![]() .则
.则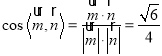 ,
,
结合图形可知,二面角![]() 为锐角,其余弦值为
为锐角,其余弦值为![]() .
.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:
【题目】袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是![]()
![]()
A. 至少有一个白球;都是白球 B. 至少有一个白球;至少有一个红球
C. 至少有一个白球;红、黑球各一个 D. 恰有一个白球;一个白球一个黑球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有1998名运动员号码为1~1998这1998个自然数,从中选出若干名运动员参加仪仗队,但要使剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.那么,选为仪仗队的运动员至少能有多少人?给出你的选取方案,并简述理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校研究性学习小组发现,学生上课的注意力指标随着听课时间的变化而变化.老师讲课开始时学生的兴趣激增,接下来学生的兴趣将保持较理想的状态一段时间,随后学生的注意力开始分散.该小组发现注意力指标![]() 与上课时刻第
与上课时刻第![]() 分钟末的关系如下(
分钟末的关系如下(![]() ,设上课开始时,t=0):
,设上课开始时,t=0): .若上课后第5分钟末时的注意力指标为140.
.若上课后第5分钟末时的注意力指标为140.
(1)求![]() 的值;
的值;
(2)上课后第5分钟末和第35分钟末比较,哪个时刻注意力更集中?
(3)在一节课中,学生的注意力指标至少达到140的时间能保持多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且数列
,且数列![]() 是单调递增数列,求实数a的取值范围;
是单调递增数列,求实数a的取值范围;
(3)若![]() ,
,![]() ,对于任意给定的正整数k,是否都存在正整数p、q,使得
,对于任意给定的正整数k,是否都存在正整数p、q,使得![]() ?若存在,试求出p、q的一组值(不论有多少组,只要求出一组即可);若不存在,请说明理由.
?若存在,试求出p、q的一组值(不论有多少组,只要求出一组即可);若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com