
【题目】已知正三棱锥的高为6,侧面与底面成![]() 的二面角,则其内切球(与四个面都相切)的表面积为( )
的二面角,则其内切球(与四个面都相切)的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
过点P作PD⊥平面ABC于D,连结并延长AD交BC于E,连结PE,△ABC是正三角形,AE是BC边上的高和中线,D为△ABC的中心.由此能求出棱锥的全面积,再求出棱锥的体积,设球的半径为r,以球心O为顶点,棱锥的四个面为底面把正三棱锥分割为四个小棱锥,利用等体积能求出球的表面积.
如图,过点P作PD⊥平面ABC于D,
连结并延长AD交BC于E,连结PE,△ABC是正三角形,
∴AE是BC边上的高和中线,D为△ABC的中心.
∴![]() 为侧面与底面所成的二面角的平面角,
为侧面与底面所成的二面角的平面角,
∴![]() =
=![]()
∵PD=6,∴DE=2![]() ,PE=4
,PE=4![]() , AB=12,
, AB=12,
∴S△ABC=![]() ×(12)2=36
×(12)2=36![]() ,S△PAB=S△PBC=S△PCA=
,S△PAB=S△PBC=S△PCA=![]() =24
=24![]() .
.
∴S表=108![]() .
.
设球的半径为r,以球心O为顶点,棱锥的四个面为底面把正三棱锥分割为四个小棱锥,
∵PD=6,∴VP﹣ABC=![]() 36
36![]() 6=72
6=72![]() .
.
则由等体积可得r=![]() =2,
=2,
∴S球=4π22=16π.
故选B.


科目:高中数学 来源: 题型:
【题目】设A,B分别为双曲线![]() (a>0,b>0)的左、右顶点,双曲线的实轴长为4
(a>0,b>0)的左、右顶点,双曲线的实轴长为4![]() ,焦点到渐近线的距离为
,焦点到渐近线的距离为![]() .
.
(1)求双曲线的方程;
(2)已知直线y=![]() x-2与双曲线的右支交于M,N两点,且在双曲线的右支上存在点D,使
x-2与双曲线的右支交于M,N两点,且在双曲线的右支上存在点D,使![]() ,求t的值及点D的坐标.
,求t的值及点D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
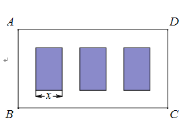
【题目】某广场要划出一块矩形区域![]() ,在其中开辟三块完全相同的矩形绿化园圃,空白处均铺设
,在其中开辟三块完全相同的矩形绿化园圃,空白处均铺设![]() 宽的走道,如图.已知三块园圃的总面积为
宽的走道,如图.已知三块园圃的总面积为![]() ,设园圃小矩形的一边长为
,设园圃小矩形的一边长为![]() ,区域
,区域![]() 的面积为
的面积为![]() (单位:
(单位:![]() ).
).
(1)求![]() 的最小值.
的最小值.
(2)若区域![]() 的面积不超过
的面积不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复平面内平行四边形ABCD(A,B,C,D按逆时针排列),A点对应的复数为2+i,向量![]() 对应的复数为1+2i,向量
对应的复数为1+2i,向量![]() 对应的复数为3-i.
对应的复数为3-i.
(1)求点C,D对应的复数.
(2)求平行四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是______(填序号).
①有两个面互相平行,其余各面都是四边形的几何体是棱柱;
②有两个面互相平行,其余各面都是平行四边形的几何体是棱柱;
③有一个面是多边形,其余各面都是三角形的几何体是棱锥;
④用一个平面去截棱锥,棱锥底面和截面之间那部分的几何体是棱台;
⑤存在一个四棱锥,其四个侧面都是直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com