Question

已知动圆过定点(,0),且与直线x=相切,其中p＞0.

(1)求动圆圆心C的轨迹方程;

(2)设A、B是轨迹C上异于原点O的两个不同点,直线OA和OB的倾斜角分别为α和β,当α、β变化且α+β为定值θ(0＜θ＜π)时,证明直线AB恒过定点,并求出该定点的坐标.

Answer 1

思路解析:此题是圆锥曲线的综合题,(1)动点的轨迹方程求解时,常常结合其满足的几何特征及常见圆锥曲线的定义来分析比较容易,即常用数形结合的方法.(2)直线过定点问题必须引入参数表示出直线的方程,由直线系方程来解.

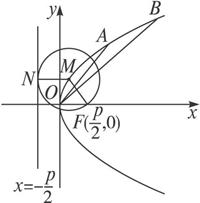
(1)解:如图,设M为动圆圆心,(,0)记为F,过点M作直线x=的垂线,垂足为N,由题意知|MF|=|MN|,即动点M到定点F与定直线x=的距离相等,由抛物线的定义,知点M的轨迹为抛物线,其中F(,0)为焦点,x=-为准线,所以轨迹方程为y²=2px(p＞0).

(2)证明:如图,设A(x₁,y₁)、B(x₂,y₂),

由题意得x₁≠x₂(否则α+β=π)且x₁、x₂≠0.

所以直线AB的斜率存在,设其方程为y=kx+b.

显然x₁=,x₂=.

将y=kx+b与y²=2px(p＞0)联立消去x,得ky²-2py+2pb=0.

由韦达定理知y₁+y₂=,y₁·y₂=.                                       ①

当θ=,即α+β=时,tanα·tanβ=1.

所以=1,x₁x₂-y₁y₂=0,

-y₁y₂=0,所以y₁y₂=4p².

由①知=4p²,所以b=2pk.

因此直线AB的方程可表示为y=kx+2pk,

即k(x+2p)-y=0.所以直线AB恒过定点(-2p,0).

当θ≠,由α+β=θ,得tanθ=tan(α+β)=.

将①式代入上式整理化简可得tanθ=,

所以b=+2pk.

此时,直线AB的方程可表示为y=kx++2pk,

即k(x+2p)-(y-)=0.

所以直线AB恒过定点(-2p,).

所以,当θ=时,直线AB恒过定点(-2p,0),

当θ≠时直线AB恒过定点(-2p,).