
已知圆的内接四边形ABCD的边长分别为AB=2,BC=6, CD=DA=4,
(1)求角A的大小;
(2)求四边形ABCD的面积.
(1)A=120º(2)8
【解析】
试题分析:(1)解三角形问题,一般利用正余弦定理进行边角转化. 由面积公式有四边形ABCD的面积S=S△ABD+S△BCD= AB·AD·sinA+
AB·AD·sinA+ BC·CD·sinC,∵A+C=180º∴sinA=sinC∴S=16sinA.由余弦定理得:BD2=AB2+AD2-2AB·AD·cosA=20-16cosA,BD2=CB2+CD2-2CB·CD·cosC=52-48cosC,∴20-16cosA=52-48cosC解之:cosA=-
BC·CD·sinC,∵A+C=180º∴sinA=sinC∴S=16sinA.由余弦定理得:BD2=AB2+AD2-2AB·AD·cosA=20-16cosA,BD2=CB2+CD2-2CB·CD·cosC=52-48cosC,∴20-16cosA=52-48cosC解之:cosA=- , 又0º<A<180º, ∴A=120º,(2)由(1)有四边形ABCD的面积S=16
, 又0º<A<180º, ∴A=120º,(2)由(1)有四边形ABCD的面积S=16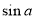 ,所以S=16sin120º=8
,所以S=16sin120º=8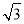 .
.
【解析】
四边形ABCD的面积S=S△ABD+S△BCD=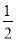 AB·AD·sinA+
AB·AD·sinA+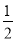 BC·CD·sinC
BC·CD·sinC
∵A+C=180º∴sinA=sinC∴S=16sinA.
由余弦定理得:BD2=AB2+AD2-2AB·AD·cosA=20-16cosA,
BD2=CB2+CD2-2CB·CD·cosC=52-48cosC,
∴20-16cosA=52-48cosC解之:cosA=-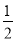 ,
,
又0º<A<180º, ∴A=120º,S=16sin120º=8
考点:正余弦定理,三角形面积公式


科目:高中数学 来源:2016届江苏省高一下学期期末模拟数学试卷(解析版) 题型:填空题
已知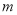 ,
, 是不重合的两条直线,
是不重合的两条直线,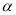 ,
,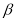 是不重合的两个平面.下列命题:①若
是不重合的两个平面.下列命题:①若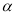 ⊥
⊥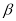 ,
, ⊥
⊥ ,则
,则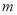 ∥
∥ ; ②若
; ②若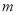 ⊥
⊥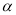 ,
,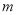 ⊥
⊥ ,则
,则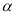 ∥
∥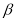 ;③若
;③若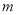 ∥
∥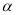 ,
,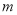 ⊥
⊥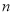 ,则
,则 ⊥
⊥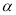 ;④若
;④若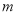 ∥
∥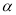 ,
, ,则
,则 ∥
∥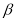 .其中所有真命题的序号是 .
.其中所有真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高一下学期期末模拟数学试卷1(解析版) 题型:填空题
已知△ABC为等腰直角三角形,斜边BC上的中线AD = 2,将△ABC沿AD折成60°的二面角,连结BC,则三棱锥C ? ABD的体积为 .
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高一下学期期中考试数学试卷(解析版) 题型:填空题
已知等差数列{an}的前n项和为Sn=(a+1)n2+a,某三角形三边之比为a2∶a3∶a4,则该三角形的最大角为________.
查看答案和解析>>
科目:高中数学 来源:2016届江苏省徐州市五县二区高一期中考试数学试卷(解析版) 题型:填空题
已知-7,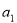 ,
, ,-1四个实数成等差数列,-4,
,-1四个实数成等差数列,-4,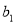 ,
,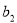 ,
, ,-1五个实数成等
,-1五个实数成等
比数列,则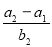 = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com