若函数f(x)=x2-x+b,且f(log2a)=b,log2f(a)=2,其中a>0且a≠1;
(1)求函数f(x)的解析式;
(2)若x∈[2,4],求函数f (log2x)的最小值及相应x的值.
【答案】
分析:(1)由f(log
2a)=b可求出a,再由log
2f(a)=2即可求得b,从而求出解析式;
(2)表示出f (log
2x),配方后利用函数单调性可求最小值及x值.
解答:解:(1)由f(log
2a)=b,得
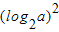
-log
2a+b=b,即
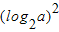
-log
2a=0,
解得,log
2a=1或log
2a=0(舍),所以a=2.
由log
2f(a)=2,得f(a)=4,即f(2)=4,
所以2
2-2+b=4,解得b=2.
所以函数f(x)=x
2-x+2.
(2)f(log
2x)=
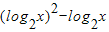
+2=
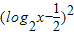
+

,
∵x∈[2,4],∴log
2x∈[1,2],
∴当log
2x=1,即x=2时,f(log
2x)的最小值为2.
点评:本题考查复合函数的单调性及二次函数的性质,属中档题.

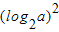 -log2a+b=b,即
-log2a+b=b,即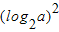 -log2a=0,
-log2a=0,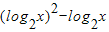 +2=
+2=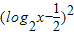 +
+ ,
,
