练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(z)＝|1＋z|－，且f(－x)＝10＋3i，则复数z＝_________．

    答案：5－3i
    解析：

    　　设z＝x＋yi(x、y∈R)，

    　　则－z＝－x－yi，由f(－z)＝10＋3i，得

    　　|1＋(－z)|－()＝10＋3i，

    　　|(1－x)－yi|－(－x＋yi)＝10＋3i，

    　　∴

    　　解之，得x＝5，y＝－3．

    　　∴所求z＝5－3i．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    已知f(x)＝＋，并且x≠2kπ＋，k∈Z；．

    (1)化简f(x)；

    (2)是否存在x，使得tan·f(x)与相等？若存在，求x的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：吉林省长春外国语学校2008-2009学年高二下学期第一次月考数学试卷 题型：044

    已知f(z)＝|1＋z|－，且f(－z)＝10＋3i，求复数z．

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　北师大课标高二版(选修1－2)　2009－2010学年　第38期　总第194期 北师大课标 题型：044

    已知f(z)＝|1＋z|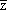－，且f(－z)＝10＋3i，求复数z．

    查看答案和解析>>

    科目：高中数学 来源：吉林省长春外国语学校2012届高三上学期期中考试数学文科试题 题型：044

    已知函数y＝f(x)的定义域为R，对任意的x，y∈R，都有f(x＋y)＝f(x)＋f(y)，对任意的x＞0，都有f(x)＜0，且f(3)＝－3

    (1)证明函数y＝f(x)在R上是减函数．

    (2)证明函数y＝f(x)是奇函数．

    (3)试求y＝f(x)在区间[m，n](m，n∈Z且mn＜0)上的值域．

    查看答案和解析>>

    同步练习册答案