
【题目】已知圆A:x2+y2+2x-15=0和定点B(1,0),M是圆A上任意一点,线段MB的垂直平分线交MA于点N,设点N的轨迹为C.
(Ⅰ)求C的方程;
(Ⅱ)若直线y=k(x-1)与曲线C相交于P,Q两点,试问:在x轴上是否存在定点R,使当k变化时,总有∠ORP=∠ORQ?若存在,求出点R的坐标;若不存在,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)存在定点R(4,0)满足题设.
;(Ⅱ)存在定点R(4,0)满足题设.
【解析】
(Ⅰ)求出圆心A,通过|NM|=|NB|,推出点N的轨迹是以A,B为焦点的椭圆,设其标准方程,求出a,c,即可求解椭圆方程.(Ⅱ)设存在点R(t,0)满足题设,联立直线y=k(x﹣1)与椭圆方程,设P(x1,y1),Q(x2,y2),利用韦达定理,通过直线RP与直线RQ的斜率之和为零,即可得到t的值.
解:(Ⅰ)圆A:(x+1)2+y2=16,圆心A(-1,0),由已知得|NM|=|NB|,
又|NM|+|NB|=4,所以|NA|+|NB|=4>|AB|=2,
所以由椭圆的定义知点N的轨迹是以A,B为焦点的椭圆,
设其标准方程C:![]() ,则2a=4,2c=2,所以a2=4,b2=3,
,则2a=4,2c=2,所以a2=4,b2=3,
所以曲线C:![]() ;
;
(Ⅱ)设存在点R(t,0)满足题设,联立直线y=k(x-1)与椭圆方程![]() ,
,
消去y,得(4k2+3)x2-8k2x+(4k2-12)=0,设P(x1,y1),Q(x2,y2),
则由韦达定理得![]() ①,
①,![]() ②,
②,
由题设知OR平分∠PRQ直线RP与直RQ的倾斜角互补,
即直线RP与直线RQ的斜率之和为零,即![]() ,即
,即![]() ,即2kx1x2-(1+t)k(x1+x2)+2tk=0③,
,即2kx1x2-(1+t)k(x1+x2)+2tk=0③,
把①、②代入③并化简得![]() ,即(t-4)k=0④,
,即(t-4)k=0④,
所以当k变化时④成立,只要t=4即可,所以存在定点R(4,0)满足题设.


科目:高中数学 来源: 题型:
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
女 | 18 | ||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每个国家对退休年龄都有不一样的规定,从2018年开始,我国关于延迟退休的话题一直在网上热议,为了了解市民对“延迟退休”的态度,现从某地市民中随机选取100人进行调查,调查情况如下表:
年龄段(单位:岁) |
|
|
|
|
|
|
被调查的人数 |
|
|
|
|
|
|
赞成的人数 |
|
|
|
|
|
|
(1)从赞成“延迟退休”的人中任选1人,此人年龄在![]() 的概率为
的概率为![]() ,求出表格中
,求出表格中![]() 的值;
的值;
(2)若从年龄在![]() 的参与调查的市民中按照是否赞成“延迟退休”进行分层抽样,从中抽取10人参与某项调查,然后再从这10人中随机抽取4人参加座谈会,记这4人中赞成“延迟退休”的人数为
的参与调查的市民中按照是否赞成“延迟退休”进行分层抽样,从中抽取10人参与某项调查,然后再从这10人中随机抽取4人参加座谈会,记这4人中赞成“延迟退休”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·重庆高二检测)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=![]() AA1,D是棱AA1的中点.
AA1,D是棱AA1的中点.

(1)证明:平面BDC1⊥平面BDC.
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】、设![]() 是1,2,…,n的一个排列,把排在
是1,2,…,n的一个排列,把排在![]() 的左边且比
的左边且比![]() 小的数的个数为
小的数的个数为![]() (
(![]() =1,2,…n)的顺序数,如在排列6,4,5,3,2,1中,5的顺序数为1,3的顺序数为0,则在1至 8这8个数的排列中,8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列的种数为 ()
=1,2,…n)的顺序数,如在排列6,4,5,3,2,1中,5的顺序数为1,3的顺序数为0,则在1至 8这8个数的排列中,8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列的种数为 ()
A.120B.48C.144D.192
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
... | ... | ... | ... | ... | ... |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]()
![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
(3)小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从广安市某中学校的![]() 名男生中随机抽取
名男生中随机抽取![]() 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于![]() cm和
cm和![]() cm之间,将测量结果按如下方式分成八组:第一组
cm之间,将测量结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,...,第八组
,...,第八组![]() ,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为![]() 人.
人.
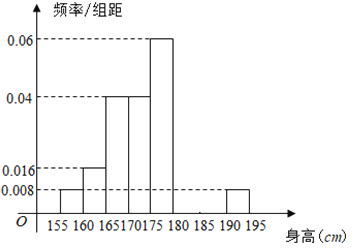
(1)求第七组的频率;
(2)估计该校![]() 名男生的身高的中位数。
名男生的身高的中位数。
(3)若从样本中身高属于第六组和第八组的所有男生中随机抽取两名男生,求抽出的两名男生是同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com